EdgeMiner¶

Added in version 1.4.

Purpose of this Module¶

This is a helper tool to:

build polylines from DXF primitives like LINE, ARC, ELLIPSE, SPLINE

build hatch boundary paths from DXF primitives

find open chains or closed loops in an unordered heap of DXF primitives (edges)

in general: find connections between edges

What are Edges?¶

An edge is a linear structure with an start- and end point and an optional length.

This module is not limited to DXF primitives. Anything that can be represented by an start- and end point can be processed. This makes this module to a versatile tool with the disadvantage that intersections between edges are not known and cannot be calculated.

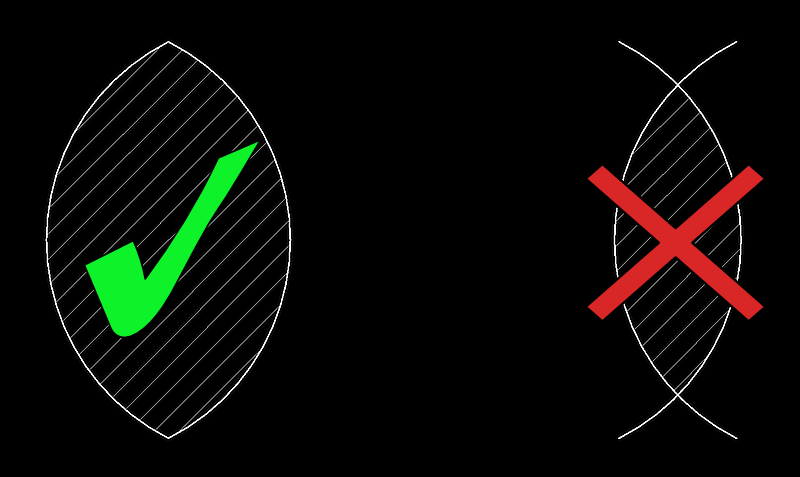
e.g. When each arc is represented by an edge, the HATCH boundary path on the left can be found because the arcs are connected by their end points. Finding the HATCH boundary path on the right is not possible because the intersections points of the arcs (edges) are not known:

How to Create Edges?¶

The process of creating edges is separated from this module and is done in the companion module ezdxf.edgesmith. The edgeminer module doesn’t really know what an edge represents or what it looks like.

Terminology¶

I try to use the terminology of Graph Theory but there are differences where I think a different term is better suited for this module like loop for cycle.

Edge: A linear connection between two points. The shape of an edge is not known. Intersection points between edges are not known and cannot be calculated.

Vertex: A connection point of two or more edges.
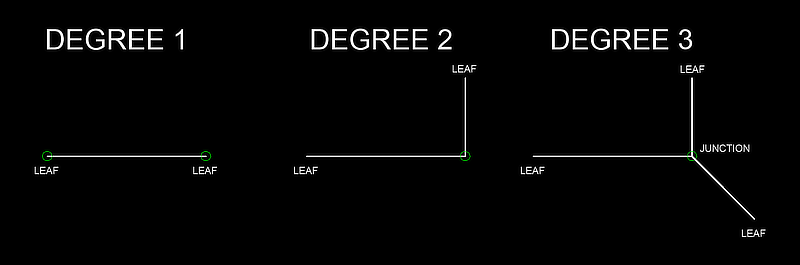
Degree: The degree of a vertex is the number of connected edges.

Leaf: A leaf is a vertex of degree 1. A leaf is a loose end of an edge, which is not connected to other edges.
Junction: A junction is a vertex of degree greater 2. A junction has more than two adjacent edges. A junction is an ambiguity when searching for open chains or closed loops. Graph Theory: multiple adjacency
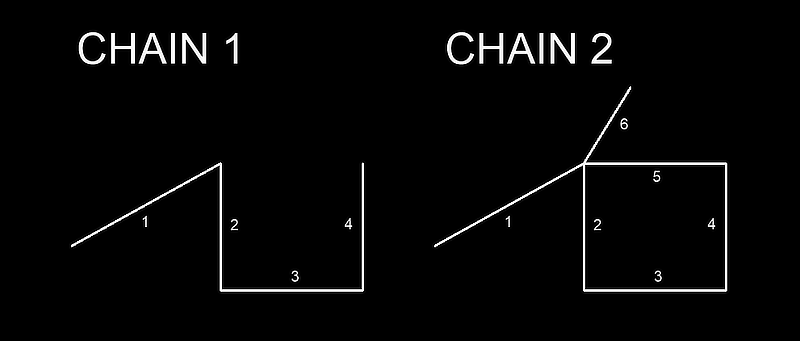
Chain: A chain has sequential connected edges. The end point of an edge is connected to the start point of the following edge. A chain has unique edges, each edge appears only once in the chain. A chain can contain vertices of degree greater 2. A solitary edge is also a chain. Graph Theory: Trail - no edge is repeated, vertex is repeated

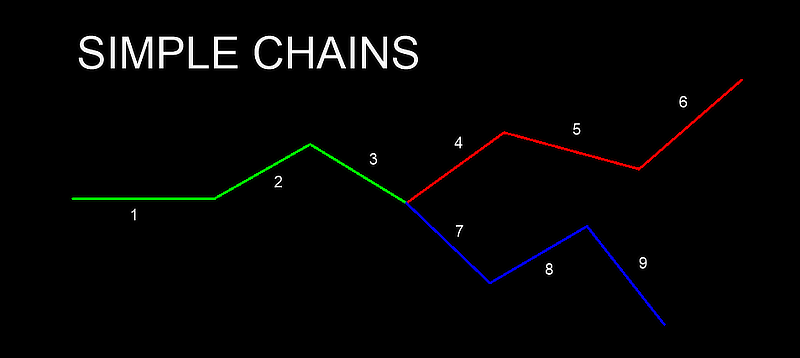
Simple Chain (special to this module): A simple chain contains only vertices of degree 2, except the start- and end vertex. The start- and end vertices are leafs (degree of 1) or junctions (degree greater 2). The following image shows 3 simple chains: [1-2-3], [4-5-6] and [7-8-9]. Simple chains are easy to detect and can be replaced by a single edge and reduces so the search space.

Open Chain: An open chain is a chain which starts and ends with a leaf. A solitary edge is also an open chain. Graph Theory: Path - no edge is repeated, no vertex is repeated, endings not connected
Loop: A loop is a simple chain with connected start- and end vertices. A loop has two or more edges. A loop contains only vertices of degree 2. Graph Theory: Cycle - no edge is repeated, no vertex is repeated, endings connected; a loop in Graph Theory is something different!
Network: A network has two or more edges that are directly and indirectly connected. The edges in a network have no order. A network can contain vertices of degree greater 2 (junctions). A solitary edge is not a network. A chain with two or more edges is a network. Graph Theory: multigraph; a network in Graph Theory is something different!
Gap Tolerance: Maximum vertex distance to consider two edges as connected
Forward Connection: An edge is forward connected when the end point of the edge is connected to the start point of the following edge.

High Level Functions¶

ezdxf.edgeminer.find_sequential_chain(edges: Sequence[Edge], *, gap_tol=GAP_TOL) → Sequence[Edge]¶

Returns a simple chain beginning at the first edge.

The search stops at the first edge without a forward connection from the previous edge. Edges will be reversed if required to create connection.

Parameters:

edges – edges to be examined
gap_tol – maximum vertex distance to consider two edges as connected

Raises:

TypeError – invalid data in sequence edges

ezdxf.edgeminer.find_all_sequential_chains(edges: Sequence[Edge], *, gap_tol=GAP_TOL) → Iterator[Sequence[Edge]]¶

Yields all simple chains from sequence edges.

The search progresses strictly in order of the input sequence. The search starts a new chain at every edge without a forward connection from the previous edge. Edges will be reversed if required to create connection. Each chain has one or more edges.

Parameters:

edges – sequence of edges
gap_tol – maximum vertex distance to consider two edges as connected

Raises:

TypeError – invalid data in sequence edges

ezdxf.edgeminer.find_simple_chain(deposit: Deposit, start: Edge) → Sequence[Edge]¶

Returns a simple chain containing start edge.

A simple chain start and ends at a leaf or a junction.

All connected edges have vertices of degree 2, except the first and last vertex. The first and the last vertex have a degree of 1 (leaf) or greater 2 (junction).

ezdxf.edgeminer.find_all_simple_chains(deposit: Deposit) → Sequence[Sequence[Edge]]¶

Returns all simple chains from deposit.

Each chains starts and ends at a leaf (degree of 1) or a junction (degree greater 2). All vertices between the start- and end vertex have a degree of 2. The result doesn’t include reversed solutions.

ezdxf.edgeminer.find_all_open_chains(deposit: Deposit, timeout: float = TIMEOUT) → Sequence[Sequence[Edge]]¶

Returns all open chains from deposit.

Returns only simple chains ending on both sides with a leaf. A leaf is a vertex of degree 1 without further connections. All vertices have a degree of 2 except for the leafs at the start and end. The result does not include reversed solutions or closed loops.

Note

This is a recursive backtracking algorithm with time complexity of O(n!).

Parameters:

deposit (Deposit) – edge deposit
timeout (float) – timeout in seconds

Raises:

TimeoutError – search process has timed out

ezdxf.edgeminer.find_loop(deposit: Deposit, *, timeout: float = TIMEOUT) → Sequence[Edge]¶

Returns the first closed loop in deposit.

Returns only simple loops, where all vertices have a degree of 2 (only two adjacent edges).

Note

This is a recursive backtracking algorithm with time complexity of O(n!).

Parameters:

deposit (Deposit) – edge deposit
timeout (float) – timeout in seconds

Raises:

TimeoutError – search process has timed out

ezdxf.edgeminer.find_loop_by_edge(deposit: Deposit, start: Edge, clockwise=True) → Sequence[Edge]¶

Returns the first loop found including the given start edge.

Returns an empty sequence if no loop was found.

Parameters:

deposit (Deposit) – edge deposit
start (Edge) – starting edge of the search
clockwise (bool) – search orientation, counter-clockwise when False

ezdxf.edgeminer.find_all_loops(deposit: Deposit, *, timeout: float = TIMEOUT) → Sequence[Sequence[Edge]]¶

Returns all closed loops from deposit.

Returns only simple loops, where all vertices have a degree of 2 (only two adjacent edges). The result does not include reversed solutions.

Note

This is a recursive backtracking algorithm with time complexity of O(n!).

Parameters:

deposit (Deposit) – edge deposit
timeout (float) – timeout in seconds

Raises:

TimeoutError – search process has timed out

Low Level Functions¶

ezdxf.edgeminer.filter_coincident_edges(deposit: Deposit, eq_fn: Callable[[Edge, Edge], bool] = line_checker()) → Sequence[Edge]¶: Returns all edges from deposit that are not coincident to any other edge in the deposit. Coincident edges are detected by the given eq_fn function.

ezdxf.edgeminer.flatten(edges: Edge | Iterable[Edge]) → Iterator[Edge]¶: Yields all edges from any nested structure of edges as a flat stream of edges.

ezdxf.edgeminer.is_chain(edges: Sequence[Edge], *, gap_tol=GAP_TOL) → bool¶

Returns True if all edges in the sequence have a forward connection.

Parameters:

edges – sequence of edges
gap_tol – maximum vertex distance to consider two edges as connected

ezdxf.edgeminer.is_forward_connected(a: Edge, b: Edge, *, gap_tol=GAP_TOL) → bool¶

Returns True if the edges have a forward connection.

Forward connection: distance from a.end to b.start <= gap_tol

Parameters:

a – first edge
b – second edge
gap_tol – maximum vertex distance to consider two edges as connected

ezdxf.edgeminer.is_loop(edges: Sequence[Edge], *, gap_tol=GAP_TOL) → bool¶

Return True if the sequence of edges is a closed loop.

Parameters:

edges – sequence of edges
gap_tol – maximum vertex distance to consider two edges as connected

ezdxf.edgeminer.is_wrapped_chain(edge: Edge) → bool¶: Returns True if edge is a wrapper for linked edges.

ezdxf.edgeminer.isclose(a: Vec3, b: Vec3, *, gap_tol=GAP_TOL) → bool¶: This function should be used to test whether two vertices are close to each other to get consistent results.

ezdxf.edgeminer.length(edges: Sequence[Edge]) → float¶: Returns the length of a sequence of edges.

ezdxf.edgeminer.longest_chain(chains: Iterable[Sequence[Edge]]) → Sequence[Edge]¶: Returns the longest chain of connected edges.

Note

This function does not verify if the input sequences are connected edges!

ezdxf.edgeminer.make_edge(start: UVec, end: UVec, length: float = -1.0, *, payload: Any = None) → Edge¶

Creates a new Edge with a unique id.

Parameters:

start – start point
end – end point
length – default is the distance between start and end
payload – arbitrary data attached to the edge

ezdxf.edgeminer.reverse_chain(chain: Sequence[Edge]) → list[Edge]¶

Returns the reversed chain.

The sequence order of the edges will be reversed as well as the start- and end points of the edges.

ezdxf.edgeminer.shortest_chain(chains: Iterable[Sequence[Edge]]) → Sequence[Edge]¶: Returns the shortest chain of connected edges.

Note

This function does not verify if the input sequences are connected edges!

ezdxf.edgeminer.subtract_edges(base: Iterable[Edge], edges: Iterable[Edge]) → list[Edge]¶: Returns all edges from the iterable base that do not exist in the iterable edges e.g. remove solutions from the search space.

ezdxf.edgeminer.unwrap_simple_chain(edge: Edge) → Sequence[Edge]¶: Unwraps a simple chain which is wrapped into a single edge.

ezdxf.edgeminer.wrap_simple_chain(chain: Sequence[Edge], *, gap_tol=GAP_TOL) → Edge¶

Wraps a sequence of linked edges (simple chain) into a single edge.

Two or more linked edges required. Closed loops cannot be wrapped into a single edge.

Raises:: ValueError – less than two edges; not a chain; chain is a closed loop

Classes¶

class ezdxf.edgeminer.Edge(id: int, start: Vec3, end: Vec3, is_reverse: bool = False, length: float = 1.0, payload: Any = None)¶

Represents an immutable edge.

An edge can represent any linear curve (line, elliptic arc, spline,…). Therefore, the length of the edge must be specified if the length calculation for a sequence of edges should be possible.

Intersection points between edges are not known and cannot be calculated

Important

Use only the make_edge() function to create new edges to get unique ids!

id¶

unique id

Type:: int

start¶

start vertex

Type:: Vec3

end¶

end vertex

Type:: Vec3

is_reverse¶

flag to indicate that the edge is reversed compared to its initial state

Type:: bool

length¶

length of the edge, default is 1.0

Type:: float

payload¶

arbitrary data attached to the edge, default is None

Type:: Any

__eq__(other) → bool¶: Return True if the ids of the edges are equal.

Important

An edge is equal to its reversed copy!

__hash__() → int¶

The edge id is used as hash value.

An Edge and its reversed edge have the same hash value and cannot both exist in the same set.

reversed() → Self¶

Returns a reversed copy.

The reversed edge has the same id as the source edge, because they represent the same edge.

class ezdxf.edgeminer.Deposit(edges: Sequence[Edge], *, gap_tol=GAP_TOL)¶

The edge deposit stores all available edges for further searches.

The edges and the search index are immutable after instantiation. The gap_tol attribute is mutable.

Parameters:

edges – sequence of Edge
gap_tol – maximum vertex distance to consider two edges as connected

gap_tol¶: maximum vertex distance to consider two edges as connected (mutable)

property edges: Sequence[Edge]¶: Sequence of edges stored in this deposit.

property max_degree: int¶: Returns the maximum degree of all vertices in this deposit.

degree_counter() → Counter[int]¶

Returns a Counter for the degree of all vertices.

Counter[degree] returns the count of vertices of this degree.
Counter.keys() returns all existing degrees in this deposit

A new counter will be created for every method call! The gap_tol attribute is mutable and different gap tolerances may yield different results.

degree(vertex: UVec) → int¶

Returns the degree of the given vertex.

degree of 0: not in this deposit
degree of 1: one edge is connected to this vertex
degree of 2: two edges are connected to this vertex
degree of 3: three edges … and so on

Check if a vertex exist in a deposit:

if deposit.degree(vertex): ...

degrees(vertices: Iterable[UVec]) → Sequence[int]¶: Returns the degree of the given vertices.

edges_linked_to(vertex: UVec, radius: float = -1) → Sequence[Edge]¶

Returns all edges linked to vertex in range of radius.

Parameters:

vertex – 3D search location
radius – search range, default radius is Deposit.gap_tol

find_all_networks() → Sequence[set[Edge]]¶: Returns all separated networks in this deposit in ascending order of edge count.

find_leafs() → Iterator[Edge]¶: Yields all edges that have at least one end point without connection to other edges.

find_nearest_edge(vertex: UVec) → Edge | None¶

Return the nearest edge to the given vertex.

The distance is measured to the connection line from start to end of the edge. This is not correct for edges that represent arcs or splines.

find_network(edge: Edge) → set[Edge]¶: Returns the network of all edges that are directly and indirectly linked to edge. A network has two or more edges, a solitary edge is not a network.

unique_vertices() → set[Vec3]¶

Returns all unique vertices from this deposit.

Ignores vertices that are close to another vertex (within the range of gap_tol). It is not determined which of the close vertices is returned.

e.g. if the vertices a, b are close together, you don’t know if you get a or b, but it’s guaranteed that you only get one of them

class ezdxf.edgeminer.TimeoutError(msg: str, solutions: Sequence[Sequence[Edge]] = tuple())¶

solutions¶: solutions found until time out occur

Global Constants¶

GAP_TOL = 1e-9
ABS_TOL = 1e-9
TIMEOUT = 60.0  # in seconds