Core

Math core module: ezdxf.math

These are the core math functions and classes which should be imported from ezdxf.math.

Utility Functions

`arc_angle_span_deg`	Returns the counter-clockwise angle span from start to end in degrees.
`arc_angle_span_rad`	Returns the counter-clockwise angle span from start to end in radians.
`arc_chord_length`	Returns the chord length for an arc defined by radius and the sagitta.
`arc_segment_count`	Returns the count of required segments for the approximation of an arc for a given maximum sagitta.
`area`	Returns the area of a polygon.
`closest_point`	Returns the closest point to a give base point.
`ellipse_param_span`	Returns the counter-clockwise params span of an elliptic arc from start- to end param.
`has_matrix_2d_stretching`	Returns `True` if matrix m performs a non-uniform xy-scaling.
`has_matrix_3d_stretching`	Returns `True` if matrix m performs a non-uniform xyz-scaling.
`open_uniform_knot_vector`	Returns an open (clamped) uniform knot vector for a B-spline of order and count control points.
`required_knot_values`	Returns the count of required knot-values for a B-spline of order and count control points.
`uniform_knot_vector`	Returns an uniform knot vector for a B-spline of order and count control points.
`xround`	Extended rounding function.
`gps_to_world_mercator`	Transform GPS (long/lat) to World Mercator.
`world_mercator_to_gps`	Transform World Mercator to GPS.

ezdxf.math.closest_point(base: UVec, points: Iterable[UVec]) → Vec3 | None

Returns the closest point to a give base point.

Parameters:

base – base point as Vec3 compatible object
points – iterable of points as Vec3 compatible object

ezdxf.math.uniform_knot_vector(count: int, order: int, normalize=False) → list[float]

Returns an uniform knot vector for a B-spline of order and count control points.

order = degree + 1

Parameters:

count – count of control points
order – spline order
normalize – normalize values in range [0, 1] if True

ezdxf.math.open_uniform_knot_vector(count: int, order: int, normalize=False) → list[float]

Returns an open (clamped) uniform knot vector for a B-spline of order and count control points.

order = degree + 1

Parameters:

count – count of control points
order – spline order
normalize – normalize values in range [0, 1] if True

ezdxf.math.required_knot_values(count: int, order: int) → int

Returns the count of required knot-values for a B-spline of order and count control points.

Parameters:

count – count of control points, in text-books referred as “n + 1”
order – order of B-Spline, in text-books referred as “k”

Relationship:

“p” is the degree of the B-spline, text-book notation.

k = p + 1
2 ≤ k ≤ n + 1

ezdxf.math.xround(value: float, rounding: float = 0.) → float

Extended rounding function.

The argument rounding defines the rounding limit:

0	remove fraction
0.1	round next to x.1, x.2, … x.0
0.25	round next to x.25, x.50, x.75 or x.00
0.5	round next to x.5 or x.0
1.0	round to a multiple of 1: remove fraction
2.0	round to a multiple of 2: xxx2, xxx4, xxx6 …
5.0	round to a multiple of 5: xxx5 or xxx0
10.0	round to a multiple of 10: xx10, xx20, …

Parameters:

value – float value to round
rounding – rounding limit

ezdxf.math.area(vertices: Iterable[UVec]) → float

Returns the area of a polygon.

Returns the projected area in the xy-plane for any vertices (z-axis will be ignored).

ezdxf.math.arc_angle_span_deg(start: float, end: float) → float

Returns the counter-clockwise angle span from start to end in degrees.

Returns the angle span in the range of [0, 360], 360 is a full circle. Full circle handling is a special case, because normalization of angles which describe a full circle would return 0 if treated as regular angles. e.g. (0, 360) → 360, (0, -360) → 360, (180, -180) → 360. Input angles with the same value always return 0 by definition: (0, 0) → 0, (-180, -180) → 0, (360, 360) → 0.

ezdxf.math.arc_angle_span_rad(start: float, end: float) → float

Returns the counter-clockwise angle span from start to end in radians.

Returns the angle span in the range of [0, 2π], 2π is a full circle. Full circle handling is a special case, because normalization of angles which describe a full circle would return 0 if treated as regular angles. e.g. (0, 2π) → 2π, (0, -2π) → 2π, (π, -π) → 2π. Input angles with the same value always return 0 by definition: (0, 0) → 0, (-π, -π) → 0, (2π, 2π) → 0.

ezdxf.math.arc_segment_count(radius: float, angle: float, sagitta: float) → int

Returns the count of required segments for the approximation of an arc for a given maximum sagitta.

Parameters:

radius – arc radius
angle – angle span of the arc in radians
sagitta – max. distance from the center of an arc segment to the center of its chord

ezdxf.math.arc_chord_length(radius: float, sagitta: float) → float

Returns the chord length for an arc defined by radius and the sagitta.

Parameters:

radius – arc radius
sagitta – distance from the center of the arc to the center of its base

ezdxf.math.ellipse_param_span(start_param: float, end_param: float) → float

Returns the counter-clockwise params span of an elliptic arc from start- to end param.

Returns the param span in the range [0, 2π], 2π is a full ellipse. Full ellipse handling is a special case, because normalization of params which describe a full ellipse would return 0 if treated as regular params. e.g. (0, 2π) → 2π, (0, -2π) → 2π, (π, -π) → 2π. Input params with the same value always return 0 by definition: (0, 0) → 0, (-π, -π) → 0, (2π, 2π) → 0.

Alias to function: ezdxf.math.arc_angle_span_rad()

ezdxf.math.has_matrix_2d_stretching(m: Matrix44) → bool

Returns True if matrix m performs a non-uniform xy-scaling. Uniform scaling is not stretching in this context.

Does not check if the target system is a cartesian coordinate system, use the Matrix44 property is_cartesian for that.

ezdxf.math.has_matrix_3d_stretching(m: Matrix44) → bool

Returns True if matrix m performs a non-uniform xyz-scaling. Uniform scaling is not stretching in this context.

Does not check if the target system is a cartesian coordinate system, use the Matrix44 property is_cartesian for that.

ezdxf.math.gps_to_world_mercator(longitude: float, latitude: float) → tuple[float, float]

Transform GPS (long/lat) to World Mercator.

Transform WGS84 EPSG:4326 location given as latitude and longitude in decimal degrees as used by GPS into World Mercator cartesian 2D coordinates in meters EPSG:3395.

Parameters:

longitude – represents the longitude value (East-West) in decimal degrees
latitude – represents the latitude value (North-South) in decimal degrees.

Added in version 1.3.0.

ezdxf.math.world_mercator_to_gps(x: float, y: float, tol: float = 1e-6) → tuple[float, float]

Transform World Mercator to GPS.

Transform WGS84 World Mercator EPSG:3395 location given as cartesian 2D coordinates x, y in meters into WGS84 decimal degrees as longitude and latitude EPSG:4326 as used by GPS.

Parameters:

x – coordinate WGS84 World Mercator
y – coordinate WGS84 World Mercator
tol – accuracy for latitude calculation

Added in version 1.3.0.

Bulge Related Functions

`arc_to_bulge`	Returns bulge parameters from arc parameters.
`bulge_3_points`	Returns bulge value defined by three points.
`bulge_center`	Returns center of arc described by the given bulge parameters.
`bulge_radius`	Returns radius of arc defined by the given bulge parameters.
`bulge_to_arc`	Returns arc parameters from bulge parameters.
`bulge_from_radius_and_chord`	Returns the bulge value for the given arc radius and chord length.
`bulge_from_arc_angle`	Returns the bulge value for the given arc angle.

2D Graphic Functions

`convex_hull_2d`	Returns the 2D convex hull of given points.
`distance_point_line_2d`	Returns the normal distance from point to 2D line defined by start- and end point.
`intersect_polylines_2d`	Returns the intersection points for two polylines as list of `Vec2` objects, the list is empty if no intersection points exist.
`intersection_line_line_2d`	Compute the intersection of two lines in the xy-plane.
`is_axes_aligned_rectangle_2d`	Returns `True` if the given points represent a rectangle aligned with the coordinate system axes.
`is_convex_polygon_2d`	Returns `True` if the 2D polygon is convex.
`is_point_in_polygon_2d`	Test if point is inside polygon.
`is_point_left_of_line`	Returns `True` if point is "left of line" defined by start- and end point, a colinear point is also "left of line" if argument colinear is `True`.
`is_point_on_line_2d`	Returns `True` if point is on line.
`offset_vertices_2d`	Yields vertices of the offset line to the shape defined by vertices.
`point_to_line_relation`	Returns `-1` if point is left line, `+1` if point is right of line and `0` if point is on the line.
`rytz_axis_construction`	The Rytz’s axis construction is a basic method of descriptive Geometry to find the axes, the semi-major axis and semi-minor axis, starting from two conjugated half-diameters.

ezdxf.math.convex_hull_2d(points: Iterable[UVec]) → list[Vec2]

Returns the 2D convex hull of given points.

Returns a closed polyline, first vertex is equal to the last vertex.

Parameters:: points – iterable of points, z-axis is ignored

ezdxf.math.distance_point_line_2d(point: Vec2, start: Vec2, end: Vec2) → float: Returns the normal distance from point to 2D line defined by start- and end point.

ezdxf.math.intersect_polylines_2d(p1: Sequence[Vec2], p2: Sequence[Vec2], abs_tol=1e-10) → list[Vec2]

Returns the intersection points for two polylines as list of Vec2 objects, the list is empty if no intersection points exist. Does not return self intersection points of p1 or p2. Duplicate intersection points are removed from the result list, but the list does not have a particular order! You can sort the result list by result.sort() to introduce an order.

Parameters:

p1 – first polyline as sequence of Vec2 objects
p2 – second polyline as sequence of Vec2 objects
abs_tol – absolute tolerance for comparisons

ezdxf.math.intersection_line_line_2d(line1: Sequence[Vec2], line2: Sequence[Vec2], virtual=True, abs_tol=TOLERANCE) → Vec2 | None

Compute the intersection of two lines in the xy-plane.

Parameters:

line1 – start- and end point of first line to test e.g. ((x1, y1), (x2, y2)).
line2 – start- and end point of second line to test e.g. ((x3, y3), (x4, y4)).
virtual – True returns any intersection point, False returns only real intersection points.
abs_tol – tolerance for intersection test.

Returns:

None if there is no intersection point (parallel lines) or intersection point as Vec2

ezdxf.math.is_axes_aligned_rectangle_2d(points: list[Vec2]) → bool

Returns True if the given points represent a rectangle aligned with the coordinate system axes.

The sides of the rectangle must be parallel to the x- and y-axes of the coordinate system. The rectangle can be open or closed (first point == last point) and oriented clockwise or counter-clockwise. Only works with 4 or 5 vertices, rectangles that have sides with collinear edges are not considered rectangles.

Added in version 1.2.0.

ezdxf.math.is_convex_polygon_2d(polygon: list[Vec2], *, strict=False, epsilon=1e-6) → bool

Returns True if the 2D polygon is convex.

This function supports open and closed polygons with clockwise or counter-clockwise vertex orientation.

Coincident vertices will always be skipped and if argument strict is True, polygons with collinear vertices are not considered as convex.

This solution works only for simple non-self-intersecting polygons!

ezdxf.math.is_point_in_polygon_2d(point: Vec2, polygon: list[Vec2], abs_tol=TOLERANCE) → int

Test if point is inside polygon. Returns +1 for inside, 0 for on the boundary and -1 for outside.

Supports convex and concave polygons with clockwise or counter-clockwise oriented polygon vertices. Does not raise an exception for degenerated polygons.

Parameters:

point – 2D point to test as Vec2
polygon – list of 2D points as Vec2
abs_tol – tolerance for distance check

Returns:

+1 for inside, 0 for on the boundary, -1 for outside

ezdxf.math.is_point_left_of_line(point: Vec2, start: Vec2, end: Vec2, colinear=False) → bool

Returns True if point is “left of line” defined by start- and end point, a colinear point is also “left of line” if argument colinear is True.

Parameters:

point – 2D point to test as Vec2
start – line definition point as Vec2
end – line definition point as Vec2
colinear – a colinear point is also “left of line” if True

ezdxf.math.is_point_on_line_2d(point: Vec2, start: Vec2, end: Vec2, ray=True, abs_tol=TOLERANCE) → bool

Returns True if point is on line.

Parameters:

point – 2D point to test as Vec2
start – line definition point as Vec2
end – line definition point as Vec2
ray – if True point has to be on the infinite ray, if False point has to be on the line segment
abs_tol – tolerance for on the line test

ezdxf.math.offset_vertices_2d(vertices: Iterable[UVec], offset: float, closed: bool = False) → Iterable[Vec2]

Yields vertices of the offset line to the shape defined by vertices. The source shape consist of straight segments and is located in the xy-plane, the z-axis of input vertices is ignored. Takes closed shapes into account if argument closed is True, which yields intersection of first and last offset segment as first vertex for a closed shape. For closed shapes the first and last vertex can be equal, else an implicit closing segment from last to first vertex is added. A shape with equal first and last vertex is not handled automatically as closed shape.

Warning

Adjacent collinear segments in opposite directions, same as a turn by 180 degree (U-turn), leads to unexpected results.

Parameters:

vertices – source shape defined by vertices
offset – line offset perpendicular to direction of shape segments defined by vertices order, offset > 0 is ‘left’ of line segment, offset < 0 is ‘right’ of line segment
closed – True to handle as closed shape

source = [(0, 0), (3, 0), (3, 3), (0, 3)]
result = list(offset_vertices_2d(source, offset=0.5, closed=True))

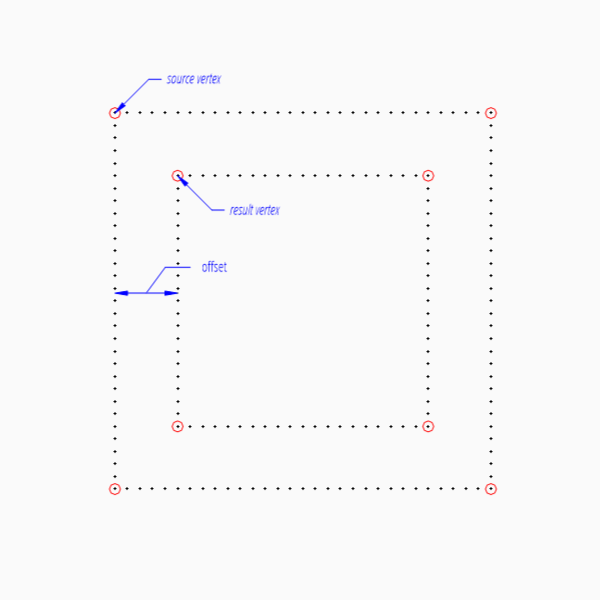
Example for a closed collinear shape, which creates 2 additional vertices and the first one has an unexpected location:

source = [(0, 0), (0, 1), (0, 2), (0, 3)]
result = list(offset_vertices_2d(source, offset=0.5, closed=True))

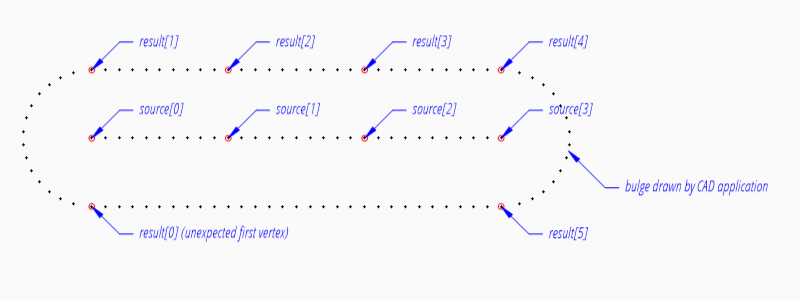
ezdxf.math.point_to_line_relation(point: Vec2, start: Vec2, end: Vec2, abs_tol=TOLERANCE) → int

Returns -1 if point is left line, +1 if point is right of line and 0 if point is on the line. The line is defined by two vertices given as arguments start and end.

Parameters:

point – 2D point to test as Vec2
start – line definition point as Vec2
end – line definition point as Vec2
abs_tol – tolerance for minimum distance to line

ezdxf.math.rytz_axis_construction(d1: Vec3, d2: Vec3) → tuple[Vec3, Vec3, float]

The Rytz’s axis construction is a basic method of descriptive Geometry to find the axes, the semi-major axis and semi-minor axis, starting from two conjugated half-diameters.

Source: Wikipedia

Given conjugated diameter d1 is the vector from center C to point P and the given conjugated diameter d2 is the vector from center C to point Q. Center of ellipse is always (0, 0, 0). This algorithm works for 2D/3D vectors.

Parameters:

d1 – conjugated semi-major axis as Vec3
d2 – conjugated semi-minor axis as Vec3

Returns:

Tuple of (major axis, minor axis, ratio)

3D Graphic Functions

`basic_transformation`	Returns a combined transformation matrix for translation, scaling and rotation about the z-axis.
`best_fit_normal`	Returns the "best fit" normal for a plane defined by three or more vertices.
`bezier_to_bspline`	Convert multiple quadratic or cubic Bèzier curves into a single cubic B-spline.
`closed_uniform_bspline`	Creates a closed uniform (periodic) B-spline curve (open curve).
`cubic_bezier_bbox`	Returns the `BoundingBox` of a cubic Bézier curve of type `Bezier4P`.
`cubic_bezier_from_3p`	Returns a cubic Bèzier curve `Bezier4P` from three points.
`cubic_bezier_from_arc`	Returns an approximation for a circular 2D arc by multiple cubic Bézier-curves.
`cubic_bezier_from_ellipse`	Returns an approximation for an elliptic arc by multiple cubic Bézier-curves.
`cubic_bezier_interpolation`	Returns an interpolation curve for given data points as multiple cubic Bézier-curves.
`distance_point_line_3d`	Returns the normal distance from a point to a 3D line.
`estimate_end_tangent_magnitude`	Estimate tangent magnitude of start- and end tangents.
`estimate_tangents`	Estimate tangents for curve defined by given fit points.
`fit_points_to_cad_cv`	Returns a cubic `BSpline` from fit points as close as possible to common CAD applications like BricsCAD.
`fit_points_to_cubic_bezier`	Returns a cubic `BSpline` from fit points without end tangents.
`global_bspline_interpolation`	B-spline interpolation by the Global Curve Interpolation.
`have_bezier_curves_g1_continuity`	Return `True` if the given adjacent Bézier curves have G1 continuity.
`intersect_polylines_3d`	Returns the intersection points for two polylines as list of `Vec3` objects, the list is empty if no intersection points exist.
`intersection_line_line_3d`	Returns the intersection point of two 3D lines, returns `None` if lines do not intersect.
`intersection_line_polygon_3d`	Returns the intersection point of the 3D line form start to end and the given polygon.
`intersection_ray_polygon_3d`	Returns the intersection point of the infinite 3D ray defined by origin and the direction vector and the given polygon.
`intersection_ray_ray_3d`	Calculate intersection of two 3D rays, returns a 0-tuple for parallel rays, a 1-tuple for intersecting rays and a 2-tuple for not intersecting and not parallel rays with points of the closest approach on each ray.
`is_planar_face`	Returns `True` if sequence of vectors is a planar face.
`is_vertex_order_ccw_3d`	Returns `True` when the given 3D vertices have a counter-clockwise order around the given normal vector.
`linear_vertex_spacing`	Returns count evenly spaced vertices from start to end.
`local_cubic_bspline_interpolation`	B-spline interpolation by 'Local Cubic Curve Interpolation', which creates B-spline from fit points and estimated tangent direction at start-, end- and passing points.
`normal_vector_3p`	Returns normal vector for 3 points, which is the normalized cross product for: `a->b x a->c`.
`open_uniform_bspline`	Creates an open uniform (periodic) B-spline curve (open curve).
`quadratic_bezier_bbox`	Returns the `BoundingBox` of a quadratic Bézier curve of type `Bezier3P`.
`quadratic_bezier_from_3p`	Returns a quadratic Bèzier curve `Bezier3P` from three points.
`quadratic_to_cubic_bezier`	Convert quadratic Bèzier curves (`ezdxf.math.Bezier3P`) into cubic Bèzier curves (`ezdxf.math.Bezier4P`).
`rational_bspline_from_arc`	Returns a rational B-splines for a circular 2D arc.
`rational_bspline_from_ellipse`	Returns a rational B-splines for an elliptic arc.
`safe_normal_vector`	Safe function to detect the normal vector for a face or polygon defined by 3 or more vertices.
`spherical_envelope`	Calculate the spherical envelope for the given points.
`split_bezier`	Split a Bèzier curve at parameter t.
`split_polygon_by_plane`	Split a convex polygon by the given plane.
`subdivide_face`	Subdivides faces by subdividing edges and adding a center vertex.
`subdivide_ngons`	Subdivides faces into triangles by adding a center vertex.

Transformation Classes

`Matrix44`	An optimized 4x4 transformation matrix.
`OCS`	Establish an OCS for a given extrusion vector.
`UCS`	Establish a user coordinate system (UCS).

OCS Class

class ezdxf.math.OCS(extrusion: UVec = Z_AXIS)

Establish an OCS for a given extrusion vector.

Parameters:: extrusion – extrusion vector.

ux: x-axis unit vector

uy: y-axis unit vector

uz: z-axis unit vector

from_wcs(point: UVec) → Vec3: Returns OCS vector for WCS point.

points_from_wcs(points: Iterable[UVec]) → Iterator[Vec3]: Returns iterable of OCS vectors from WCS points.

to_wcs(point: UVec) → Vec3: Returns WCS vector for OCS point.

points_to_wcs(points: Iterable[UVec]) → Iterator[Vec3]: Returns iterable of WCS vectors for OCS points.

render_axis(layout: BaseLayout, length: float = 1, colors: RGB = RGB(1, 3, 5)) → None: Render axis as 3D lines into a layout.

UCS Class

class ezdxf.math.UCS(origin: UVec = (0, 0, 0), ux: UVec | None = None, uy: UVec | None = None, uz: UVec | None = None)

Establish a user coordinate system (UCS). The UCS is defined by the origin and two unit vectors for the x-, y- or z-axis, all axis in WCS. The missing axis is the cross product of the given axis.

If x- and y-axis are None: ux = (1, 0, 0), uy = (0, 1, 0), uz = (0, 0, 1).

Unit vectors don’t have to be normalized, normalization is done at initialization, this is also the reason why scaling gets lost by copying or rotating.

Parameters:

origin – defines the UCS origin in world coordinates
ux – defines the UCS x-axis as vector in WCS
uy – defines the UCS y-axis as vector in WCS
uz – defines the UCS z-axis as vector in WCS

ux: x-axis unit vector

uy: y-axis unit vector

uz: z-axis unit vector

is_cartesian: Returns True if cartesian coordinate system.

copy() → UCS: Returns a copy of this UCS.

to_wcs(point: Vec3) → Vec3: Returns WCS point for UCS point.

points_to_wcs(points: Iterable[Vec3]) → Iterator[Vec3]: Returns iterable of WCS vectors for UCS points.

direction_to_wcs(vector: Vec3) → Vec3: Returns WCS direction for UCS vector without origin adjustment.

from_wcs(point: Vec3) → Vec3: Returns UCS point for WCS point.

points_from_wcs(points: Iterable[Vec3]) → Iterator[Vec3]: Returns iterable of UCS vectors from WCS points.

direction_from_wcs(vector: Vec3) → Vec3: Returns UCS vector for WCS vector without origin adjustment.

to_ocs(point: Vec3) → Vec3

Returns OCS vector for UCS point.

The OCS is defined by the z-axis of the UCS.

points_to_ocs(points: Iterable[Vec3]) → Iterator[Vec3]

Returns iterable of OCS vectors for UCS points.

The OCS is defined by the z-axis of the UCS.

Parameters:: points – iterable of UCS vertices

to_ocs_angle_deg(angle: float) → float

Transforms angle from current UCS to the parent coordinate system (most likely the WCS) including the transformation to the OCS established by the extrusion vector UCS.uz.

Parameters:: angle – in UCS in degrees

transform(m: Matrix44) → UCS

General inplace transformation interface, returns self (floating interface).

Parameters:: m – 4x4 transformation matrix (ezdxf.math.Matrix44)

rotate(axis: UVec, angle: float) → UCS

Returns a new rotated UCS, with the same origin as the source UCS. The rotation vector is located in the origin and has WCS coordinates e.g. (0, 0, 1) is the WCS z-axis as rotation vector.

Parameters:

axis – arbitrary rotation axis as vector in WCS
angle – rotation angle in radians

rotate_local_x(angle: float) → UCS

Returns a new rotated UCS, rotation axis is the local x-axis.

Parameters:: angle – rotation angle in radians

rotate_local_y(angle: float) → UCS

Returns a new rotated UCS, rotation axis is the local y-axis.

Parameters:: angle – rotation angle in radians

rotate_local_z(angle: float) → UCS

Returns a new rotated UCS, rotation axis is the local z-axis.

Parameters:: angle – rotation angle in radians

shift(delta: UVec) → UCS

Shifts current UCS by delta vector and returns self.

Parameters:: delta – shifting vector

moveto(location: UVec) → UCS

Place current UCS at new origin location and returns self.

Parameters:: location – new origin in WCS

static from_x_axis_and_point_in_xy(origin: UVec, axis: UVec, point: UVec) → UCS

Returns a new UCS defined by the origin, the x-axis vector and an arbitrary point in the xy-plane.

Parameters:

origin – UCS origin as (x, y, z) tuple in WCS
axis – x-axis vector as (x, y, z) tuple in WCS
point – arbitrary point unlike the origin in the xy-plane as (x, y, z) tuple in WCS

static from_x_axis_and_point_in_xz(origin: UVec, axis: UVec, point: UVec) → UCS

Returns a new UCS defined by the origin, the x-axis vector and an arbitrary point in the xz-plane.

Parameters:

origin – UCS origin as (x, y, z) tuple in WCS
axis – x-axis vector as (x, y, z) tuple in WCS
point – arbitrary point unlike the origin in the xz-plane as (x, y, z) tuple in WCS

static from_y_axis_and_point_in_xy(origin: UVec, axis: UVec, point: UVec) → UCS

Returns a new UCS defined by the origin, the y-axis vector and an arbitrary point in the xy-plane.

Parameters:

origin – UCS origin as (x, y, z) tuple in WCS
axis – y-axis vector as (x, y, z) tuple in WCS
point – arbitrary point unlike the origin in the xy-plane as (x, y, z) tuple in WCS

static from_y_axis_and_point_in_yz(origin: UVec, axis: UVec, point: UVec) → UCS

Returns a new UCS defined by the origin, the y-axis vector and an arbitrary point in the yz-plane.

Parameters:

origin – UCS origin as (x, y, z) tuple in WCS
axis – y-axis vector as (x, y, z) tuple in WCS
point – arbitrary point unlike the origin in the yz-plane as (x, y, z) tuple in WCS

static from_z_axis_and_point_in_xz(origin: UVec, axis: UVec, point: UVec) → UCS

Returns a new UCS defined by the origin, the z-axis vector and an arbitrary point in the xz-plane.

Parameters:

origin – UCS origin as (x, y, z) tuple in WCS
axis – z-axis vector as (x, y, z) tuple in WCS
point – arbitrary point unlike the origin in the xz-plane as (x, y, z) tuple in WCS

static from_z_axis_and_point_in_yz(origin: UVec, axis: UVec, point: UVec) → UCS

Returns a new UCS defined by the origin, the z-axis vector and an arbitrary point in the yz-plane.

Parameters:

origin – UCS origin as (x, y, z) tuple in WCS
axis – z-axis vector as (x, y, z) tuple in WCS
point – arbitrary point unlike the origin in the yz-plane as (x, y, z) tuple in WCS

render_axis(layout: BaseLayout, length: float = 1, colors: RGB = RGB(1, 3, 5)): Render axis as 3D lines into a layout.

Matrix44

class ezdxf.math.Matrix44(*args)

An optimized 4x4 transformation matrix.

The utility functions for constructing transformations and transforming vectors and points assumes that vectors are stored as row vectors, meaning when multiplied, transformations are applied left to right (e.g. vAB transforms v by A then by B).

Matrix44 initialization:

Matrix44() returns the identity matrix.

Matrix44(values) values is an iterable with the 16 components of the matrix.

Matrix44(row1, row2, row3, row4) four rows, each row with four values.

__repr__() → str: Returns the representation string of the matrix in row-major order: Matrix44((col0, col1, col2, col3), (...), (...), (...))

get_row(row: int) → tuple[float, ...]

Get row as list of four float values.

Parameters:: row – row index [0 .. 3]

set_row(row: int, values: Sequence[float]) → None

Sets the values in a row.

Parameters:

row – row index [0 .. 3]
values – iterable of four row values

get_col(col: int) → tuple[float, ...]

Returns a column as a tuple of four floats.

Parameters:: col – column index [0 .. 3]

set_col(col: int, values: Sequence[float])

Sets the values in a column.

Parameters:

col – column index [0 .. 3]
values – iterable of four column values

copy() → Matrix44: Returns a copy of same type.

__copy__() → Matrix44: Returns a copy of same type.

classmethod scale(sx: float, sy: float | None = None, sz: float | None = None) → Matrix44: Returns a scaling transformation matrix. If sy is None, sy = sx, and if sz is None sz = sx.

classmethod translate(dx: float, dy: float, dz: float) → Matrix44: Returns a translation matrix for translation vector (dx, dy, dz).

classmethod x_rotate(angle: float) → Matrix44

Returns a rotation matrix about the x-axis.

Parameters:: angle – rotation angle in radians

classmethod y_rotate(angle: float) → Matrix44

Returns a rotation matrix about the y-axis.

Parameters:: angle – rotation angle in radians

classmethod z_rotate(angle: float) → Matrix44

Returns a rotation matrix about the z-axis.

Parameters:: angle – rotation angle in radians

classmethod axis_rotate(axis: UVec, angle: float) → Matrix44

Returns a rotation matrix about an arbitrary axis.

Parameters:

axis – rotation axis as (x, y, z) tuple or Vec3 object
angle – rotation angle in radians

classmethod xyz_rotate(angle_x: float, angle_y: float, angle_z: float) → Matrix44

Returns a rotation matrix for rotation about each axis.

Parameters:

angle_x – rotation angle about x-axis in radians
angle_y – rotation angle about y-axis in radians
angle_z – rotation angle about z-axis in radians

classmethod shear_xy(angle_x: float = 0, angle_y: float = 0) → Matrix44

Returns a translation matrix for shear mapping (visually similar to slanting) in the xy-plane.

Parameters:

angle_x – slanting angle in x direction in radians
angle_y – slanting angle in y direction in radians

classmethod perspective_projection(left: float, right: float, top: float, bottom: float, near: float, far: float) → Matrix44

Returns a matrix for a 2D projection.

Parameters:

left – Coordinate of left of screen
right – Coordinate of right of screen
top – Coordinate of the top of the screen
bottom – Coordinate of the bottom of the screen
near – Coordinate of the near clipping plane
far – Coordinate of the far clipping plane

classmethod perspective_projection_fov(fov: float, aspect: float, near: float, far: float) → Matrix44

Returns a matrix for a 2D projection.

Parameters:

fov – The field of view (in radians)
aspect – The aspect ratio of the screen (width / height)
near – Coordinate of the near clipping plane
far – Coordinate of the far clipping plane

static chain(*matrices: Matrix44) → Matrix44: Compose a transformation matrix from one or more matrices.

static ucs(ux: Vec3 = X_AXIS, uy: Vec3 = Y_AXIS, uz: Vec3 = Z_AXIS, origin: Vec3 = NULLVEC) → Matrix44

Returns a matrix for coordinate transformation from WCS to UCS. For transformation from UCS to WCS, transpose the returned matrix.

Parameters:

ux – x-axis for UCS as unit vector
uy – y-axis for UCS as unit vector
uz – z-axis for UCS as unit vector
origin – UCS origin as location vector

__hash__(): Return hash(self).

__getitem__(index: tuple[int, int]): Get (row, column) element.

__setitem__(index: tuple[int, int], value: float): Set (row, column) element.

__iter__() → Iterator[float]: Iterates over all matrix values.

rows() → Iterator[tuple[float, ...]]: Iterate over rows as 4-tuples.

columns() → Iterator[tuple[float, ...]]: Iterate over columns as 4-tuples.

__mul__(other: Matrix44) → Matrix44: Returns a new matrix as result of the matrix multiplication with another matrix.

__imul__(other: Matrix44) → Matrix44: Inplace multiplication with another matrix.

transform(vector: UVec) → Vec3: Returns a transformed vertex.

transform_direction(vector: UVec, normalize=False) → Vec3: Returns a transformed direction vector without translation.

transform_vertices(vectors: Iterable[UVec]) → Iterator[Vec3]: Returns an iterable of transformed vertices.

fast_2d_transform(points: Iterable[UVec]) → Iterator[Vec2]

Fast transformation of 2D points. For 3D input points the z-axis will be ignored. This only works reliable if only 2D transformations have been applied to the 4x4 matrix!

Profiling results - speed gains over transform_vertices():

pure Python code: ~1.6x

Python with C-extensions: less than 1.1x

PyPy 3.8: ~4.3x

But speed isn’t everything, returning the processed input points as Vec2 instances is another advantage.

Added in version 1.1.

transform_directions(vectors: Iterable[UVec], normalize=False) → Iterator[Vec3]: Returns an iterable of transformed direction vectors without translation.

transpose() → None: Swaps the rows for columns inplace.

determinant() → float: Returns determinant.

inverse() → None

Calculates the inverse of the matrix.

Raises:: ZeroDivisionError – if matrix has no inverse.

property is_cartesian: bool: Returns True if target coordinate system is a right handed orthogonal coordinate system.

property is_orthogonal: bool

Returns True if target coordinate system has orthogonal axis.

Does not check for left- or right handed orientation, any orientation of the axis valid.

Basic Construction Classes

`BoundingBox`	3D bounding box.
`BoundingBox2d`	2D bounding box.
`ConstructionArc`	Construction tool for 2D arcs.
`ConstructionBox`	Construction tool for 2D rectangles.
`ConstructionCircle`	Construction tool for 2D circles.
`ConstructionEllipse`	Construction tool for 3D ellipsis.
`ConstructionLine`	Construction tool for 2D lines.
`ConstructionPolyline`	Construction tool for 3D polylines.
`ConstructionRay`	Construction tool for infinite 2D rays.
`Plane`	Construction tool for 3D planes.
`Shape2d`	Construction tools for 2D shapes.
`Vec2`	Immutable 2D vector class.
`Vec3`	Immutable 3D vector class.

UVec

class ezdxf.math.UVec: Type alias for Union[Sequence[float], Vec2, Vec3]

Vec3

class ezdxf.math.Vec3(*args)

Immutable 3D vector class.

This class is optimized for universality not for speed. Immutable means you can’t change (x, y, z) components after initialization:

v1 = Vec3(1, 2, 3)
v2 = v1
v2.z = 7  # this is not possible, raises AttributeError
v2 = Vec3(v2.x, v2.y, 7)  # this creates a new Vec3() object
assert v1.z == 3  # and v1 remains unchanged

Vec3 initialization:

Vec3(), returns Vec3(0, 0, 0)

Vec3((x, y)), returns Vec3(x, y, 0)

Vec3((x, y, z)), returns Vec3(x, y, z)

Vec3(x, y), returns Vec3(x, y, 0)

Vec3(x, y, z), returns Vec3(x, y, z)

Addition, subtraction, scalar multiplication and scalar division left and right-handed are supported:

v = Vec3(1, 2, 3)
v + (1, 2, 3) == Vec3(2, 4, 6)
(1, 2, 3) + v == Vec3(2, 4, 6)
v - (1, 2, 3) == Vec3(0, 0, 0)
(1, 2, 3) - v == Vec3(0, 0, 0)
v * 3 == Vec3(3, 6, 9)
3 * v == Vec3(3, 6, 9)
Vec3(3, 6, 9) / 3 == Vec3(1, 2, 3)
-Vec3(1, 2, 3) == (-1, -2, -3)

Comparison between vectors and vectors or tuples is supported:

Vec3(1, 2, 3) < Vec3 (2, 2, 2)
(1, 2, 3) < tuple(Vec3(2, 2, 2))  # conversion necessary
Vec3(1, 2, 3) == (1, 2, 3)

bool(Vec3(1, 2, 3)) is True
bool(Vec3(0, 0, 0)) is False

x: x-axis value

y: y-axis value

z: z-axis value

xy: Vec3 as (x, y, 0), projected on the xy-plane.

xyz: Vec3 as (x, y, z) tuple.

vec2: Real 2D vector as Vec2 object.

magnitude: Length of vector.

magnitude_xy: Length of vector in the xy-plane.

magnitude_square: Square length of vector.

is_null

Vec3(0, 0, 0). Has a fixed absolute testing tolerance of 1e-12!

Type:: True if all components are close to zero

angle: Angle between vector and x-axis in the xy-plane in radians.

angle_deg: Returns angle of vector and x-axis in the xy-plane in degrees.

spatial_angle: Spatial angle between vector and x-axis in radians.

spatial_angle_deg: Spatial angle between vector and x-axis in degrees.

__str__() → str: Return '(x, y, z)' as string.

__repr__() → str: Return 'Vec3(x, y, z)' as string.

__len__() → int: Returns always 3.

__hash__() → int: Returns hash value of vector, enables the usage of vector as key in set and dict.

copy() → Vec3: Returns a copy of vector as Vec3 object.

__copy__() → Vec3: Returns a copy of vector as Vec3 object.

__deepcopy__(memodict: dict) → Vec3: copy.deepcopy() support.

__getitem__(index: int) → float

Support for indexing:

v[0] is v.x
v[1] is v.y
v[2] is v.z

__iter__() → Iterator[float]: Returns iterable of x-, y- and z-axis.

__abs__() → float: Returns length (magnitude) of vector.

replace(x: float | None = None, y: float | None = None, z: float | None = None) → Vec3: Returns a copy of vector with replaced x-, y- and/or z-axis.

classmethod generate(items: Iterable[UVec]) → Iterator[Vec3]: Returns an iterable of Vec3 objects.

classmethod list(items: Iterable[UVec]) → list[Vec3]: Returns a list of Vec3 objects.

classmethod tuple(items: Iterable[UVec]) → Sequence[Vec3]: Returns a tuple of Vec3 objects.

classmethod from_angle(angle: float, length: float = 1.0) → Vec3: Returns a Vec3 object from angle in radians in the xy-plane, z-axis = 0.

classmethod from_deg_angle(angle: float, length: float = 1.0) → Vec3: Returns a Vec3 object from angle in degrees in the xy-plane, z-axis = 0.

orthogonal(ccw: bool = True) → Vec3

Returns orthogonal 2D vector, z-axis is unchanged.

Parameters:: ccw – counter-clockwise if True else clockwise

lerp(other: UVec, factor=0.5) → Vec3

Returns linear interpolation between self and other.

Parameters:

other – end point as Vec3 compatible object
factor – interpolation factor (0 = self, 1 = other, 0.5 = mid point)

is_parallel(other: Vec3, *, rel_tol: float = 1e-9, abs_tol: float = 1e-12) → bool: Returns True if self and other are parallel to vectors.

project(other: UVec) → Vec3: Returns projected vector of other onto self.

normalize(length: float = 1.0) → Vec3: Returns normalized vector, optional scaled by length.

reversed() → Vec3: Returns negated vector (-self).

isclose(other: UVec, *, rel_tol: float = 1e-9, abs_tol: float = 1e-12) → bool

Returns True if self is close to other. Uses math.isclose() to compare all axis.

Learn more about the math.isclose() function in PEP 485.

__neg__() → Vec3: Returns negated vector (-self).

__bool__() → bool: Returns True if vector is not (0, 0, 0).

__eq__(other: UVec) → bool

Equal operator.

Parameters:: other – Vec3 compatible object

__lt__(other: UVec) → bool

Lower than operator.

Parameters:: other – Vec3 compatible object

__add__(other: UVec) → Vec3: Add Vec3 operator: self + other.

__radd__(other: UVec) → Vec3: RAdd Vec3 operator: other + self.

__sub__(other: UVec) → Vec3: Sub Vec3 operator: self - other.

__rsub__(other: UVec) → Vec3: RSub Vec3 operator: other - self.

__mul__(other: float) → Vec3: Scalar Mul operator: self * other.

__rmul__(other: float) → Vec3: Scalar RMul operator: other * self.

__truediv__(other: float) → Vec3: Scalar Div operator: self / other.

dot(other: UVec) → float

Dot operator: self . other

Parameters:: other – Vec3 compatible object

cross(other: UVec) → Vec3

Cross operator: self x other

Parameters:: other – Vec3 compatible object

distance(other: UVec) → float: Returns distance between self and other vector.

angle_about(base: UVec, target: UVec) → float

Returns counter-clockwise angle in radians about self from base to target when projected onto the plane defined by self as the normal vector.

Parameters:

base – base vector, defines angle 0
target – target vector

angle_between(other: UVec) → float

Returns angle between self and other in radians. +angle is counter clockwise orientation.

Parameters:: other – Vec3 compatible object

rotate(angle: float) → Vec3

Returns vector rotated about angle around the z-axis.

Parameters:: angle – angle in radians

rotate_deg(angle: float) → Vec3

Returns vector rotated about angle around the z-axis.

Parameters:: angle – angle in degrees

static sum(items: Iterable[UVec]) → Vec3: Add all vectors in items.

ezdxf.math.X_AXIS: Vec3(1, 0, 0)

ezdxf.math.Y_AXIS: Vec3(0, 1, 0)

ezdxf.math.Z_AXIS: Vec3(0, 0, 1)

ezdxf.math.NULLVEC: Vec3(0, 0, 0)

Vec2

class ezdxf.math.Vec2(v=(0.0, 0.0), y=None)

Immutable 2D vector class.

Parameters:

v – vector object with x and y attributes/properties or a sequence of float [x, y, ...] or x-axis as float if argument y is not None
y – second float for Vec2(x, y)

Vec2 implements a subset of Vec3.

Plane

class ezdxf.math.Plane(normal: Vec3, distance: float)

Construction tool for 3D planes.

Represents a plane in 3D space as a normal vector and the perpendicular distance from the origin.

normal: Normal vector of the plane.

distance_from_origin: The (perpendicular) distance of the plane from origin (0, 0, 0).

vector: Returns the location vector.

classmethod from_3p(a: Vec3, b: Vec3, c: Vec3) → Plane: Returns a new plane from 3 points in space.

classmethod from_vector(vector: UVec) → Plane: Returns a new plane from the given location vector.

copy() → Plane: Returns a copy of the plane.

signed_distance_to(v: Vec3) → float: Returns signed distance of vertex v to plane, if distance is > 0, v is in ‘front’ of plane, in direction of the normal vector, if distance is < 0, v is at the ‘back’ of the plane, in the opposite direction of the normal vector.

distance_to(v: Vec3) → float: Returns absolute (unsigned) distance of vertex v to plane.

is_coplanar_vertex(v: Vec3, abs_tol=1e-9) → bool: Returns True if vertex v is coplanar, distance from plane to vertex v is 0.

is_coplanar_plane(p: Plane, abs_tol=1e-9) → bool: Returns True if plane p is coplanar, normal vectors in same or opposite direction.

intersect_line(start: Vec3, end: Vec3, *, coplanar=True, abs_tol=PLANE_EPSILON) → Vec3 | None: Returns the intersection point of the 3D line from start to end and this plane or None if there is no intersection. If the argument coplanar is False the start- or end point of the line are ignored as intersection points.

intersect_ray(origin: Vec3, direction: Vec3) → Vec3 | None: Returns the intersection point of the infinite 3D ray defined by origin and the direction vector and this plane or None if there is no intersection. A coplanar ray does not intersect the plane!

BoundingBox

class ezdxf.math.BoundingBox(vertices: Iterable[UVec] | None = None)

3D bounding box.

Parameters:: vertices – iterable of (x, y, z) tuples or Vec3 objects

extmin: “lower left” corner of bounding box

extmax: “upper right” corner of bounding box

property is_empty: bool: Returns True if the bounding box is empty or the bounding box has a size of 0 in any or all dimensions or is undefined.

property has_data: bool: Returns True if the bonding box has known limits.

property size: T: Returns size of bounding box.

property center: T: Returns center of bounding box.

inside(vertex: UVec) → bool

Returns True if vertex is inside this bounding box.

Vertices at the box border are inside!

any_inside(vertices: Iterable[UVec]) → bool

Returns True if any vertex is inside this bounding box.

Vertices at the box border are inside!

all_inside(vertices: Iterable[UVec]) → bool

Returns True if all vertices are inside this bounding box.

Vertices at the box border are inside!

has_intersection(other: AbstractBoundingBox[T]) → bool

Returns True if this bounding box intersects with other but does not include touching bounding boxes, see also has_overlap():

bbox1 = BoundingBox([(0, 0, 0), (1, 1, 1)])
bbox2 = BoundingBox([(1, 1, 1), (2, 2, 2)])
assert bbox1.has_intersection(bbox2) is False

has_overlap(other: AbstractBoundingBox[T]) → bool

Returns True if this bounding box intersects with other but in contrast to has_intersection() includes touching bounding boxes too:

bbox1 = BoundingBox([(0, 0, 0), (1, 1, 1)])
bbox2 = BoundingBox([(1, 1, 1), (2, 2, 2)])
assert bbox1.has_overlap(bbox2) is True

contains(other: AbstractBoundingBox[T]) → bool: Returns True if the other bounding box is completely inside this bounding box.

extend(vertices: Iterable[UVec]) → None

Extend bounds by vertices.

Parameters:: vertices – iterable of vertices

union(other: AbstractBoundingBox[T]) → AbstractBoundingBox[T]: Returns a new bounding box as union of this and other bounding box.

intersection(other: AbstractBoundingBox[T]) → BoundingBox: Returns the bounding box of the intersection cube of both 3D bounding boxes. Returns an empty bounding box if the intersection volume is 0.

rect_vertices() → Sequence[Vec2]: Returns the corners of the bounding box in the xy-plane as Vec2 objects.

cube_vertices() → Sequence[Vec3]: Returns the 3D corners of the bounding box as Vec3 objects.

grow(value: float) → None: Grow or shrink the bounding box by an uniform value in x, y and z-axis. A negative value shrinks the bounding box. Raises ValueError for shrinking the size of the bounding box to zero or below in any dimension.

BoundingBox2d

class ezdxf.math.BoundingBox2d(vertices: Iterable[UVec] | None = None)

2D bounding box.

Parameters:: vertices – iterable of (x, y[, z]) tuples or Vec3 objects

extmin: “lower left” corner of bounding box

extmax: “upper right” corner of bounding box

property is_empty: bool: Returns True if the bounding box is empty. The bounding box has a size of 0 in any or all dimensions or is undefined.

property has_data: bool: Returns True if the bonding box has known limits.

property size: T: Returns size of bounding box.

property center: T: Returns center of bounding box.

inside(vertex: UVec) → bool

Returns True if vertex is inside this bounding box.

Vertices at the box border are inside!

any_inside(vertices: Iterable[UVec]) → bool

Returns True if any vertex is inside this bounding box.

Vertices at the box border are inside!

all_inside(vertices: Iterable[UVec]) → bool

Returns True if all vertices are inside this bounding box.

Vertices at the box border are inside!

has_intersection(other: AbstractBoundingBox[T]) → bool

Returns True if this bounding box intersects with other but does not include touching bounding boxes, see also has_overlap():

bbox1 = BoundingBox2d([(0, 0), (1, 1)])
bbox2 = BoundingBox2d([(1, 1), (2, 2)])
assert bbox1.has_intersection(bbox2) is False

has_overlap(other: AbstractBoundingBox[T]) → bool

Returns True if this bounding box intersects with other but in contrast to has_intersection() includes touching bounding boxes too:

bbox1 = BoundingBox2d([(0, 0), (1, 1)])
bbox2 = BoundingBox2d([(1, 1), (2, 2)])
assert bbox1.has_overlap(bbox2) is True

contains(other: AbstractBoundingBox[T]) → bool: Returns True if the other bounding box is completely inside this bounding box.

extend(vertices: Iterable[UVec]) → None

Extend bounds by vertices.

Parameters:: vertices – iterable of vertices

union(other: AbstractBoundingBox[T]) → AbstractBoundingBox[T]: Returns a new bounding box as union of this and other bounding box.

intersection(other: AbstractBoundingBox[T]) → BoundingBox2d: Returns the bounding box of the intersection rectangle of both 2D bounding boxes. Returns an empty bounding box if the intersection area is 0.

rect_vertices() → Sequence[Vec2]: Returns the corners of the bounding box in the xy-plane as Vec2 objects.

ConstructionRay

class ezdxf.math.ConstructionRay(p1: UVec, p2: UVec | None = None, angle: float | None = None)

Construction tool for infinite 2D rays.

Parameters:

p1 – definition point 1
p2 – ray direction as 2nd point or None
angle – ray direction as angle in radians or None

location: Location vector as Vec2.

direction: Direction vector as Vec2.

slope: Slope of ray or None if vertical.

angle: Angle between x-axis and ray in radians.

angle_deg: Angle between x-axis and ray in degrees.

is_vertical: True if ray is vertical (parallel to y-axis).

is_horizontal: True if ray is horizontal (parallel to x-axis).

__str__(): Return str(self).

is_parallel(other: ConstructionRay) → bool: Returns True if rays are parallel.

intersect(other: ConstructionRay) → Vec2

Returns the intersection point as (x, y) tuple of self and other.

Raises:: ParallelRaysError – if rays are parallel

orthogonal(location: UVec) → ConstructionRay: Returns orthogonal ray at location.

bisectrix(other: ConstructionRay) → ConstructionRay: Bisectrix between self and other.

yof(x: float) → float

Returns y-value of ray for x location.

Raises:: ArithmeticError – for vertical rays

xof(y: float) → float

Returns x-value of ray for y location.

Raises:: ArithmeticError – for horizontal rays

ConstructionLine

class ezdxf.math.ConstructionLine(start: UVec, end: UVec)

Construction tool for 2D lines.

The ConstructionLine class is similar to ConstructionRay, but has a start- and endpoint. The direction of line goes from start- to endpoint, “left of line” is always in relation to this line direction.

Parameters:

start – start point of line as Vec2 compatible object
end – end point of line as Vec2 compatible object

start: start point as Vec2

end: end point as Vec2

bounding_box: bounding box of line as BoundingBox2d object.

ray: collinear ConstructionRay.

is_vertical: True if line is vertical.

is_horizontal: True if line is horizontal.

__str__(): Return str(self).

translate(dx: float, dy: float) → None

Move line about dx in x-axis and about dy in y-axis.

Parameters:

dx – translation in x-axis
dy – translation in y-axis

length() → float: Returns length of line.

midpoint() → Vec2: Returns mid point of line.

inside_bounding_box(point: UVec) → bool: Returns True if point is inside of line bounding box.

intersect(other: ConstructionLine, abs_tol: float = TOLERANCE) → Vec2 | None

Returns the intersection point of to lines or None if they have no intersection point.

Parameters:

other – other ConstructionLine
abs_tol – tolerance for distance check

has_intersection(other: ConstructionLine, abs_tol: float = TOLERANCE) → bool: Returns True if has intersection with other line.

is_point_left_of_line(point: UVec, colinear=False) → bool

Returns True if point is left of construction line in relation to the line direction from start to end.

If colinear is True, a colinear point is also left of the line.

ConstructionCircle

class ezdxf.math.ConstructionCircle(center: UVec, radius: float = 1.0)

Construction tool for 2D circles.

Parameters:

center – center point as Vec2 compatible object
radius – circle radius > 0

center: center point as Vec2

radius: radius as float

bounding_box: 2D bounding box of circle as BoundingBox2d object.

static from_3p(p1: UVec, p2: UVec, p3: UVec) → ConstructionCircle: Creates a circle from three points, all points have to be compatible to Vec2 class.

__str__() → str: Returns string representation of circle “ConstructionCircle(center, radius)”.

translate(dx: float, dy: float) → None

Move circle about dx in x-axis and about dy in y-axis.

Parameters:

dx – translation in x-axis
dy – translation in y-axis

point_at(angle: float) → Vec2

Returns point on circle at angle as Vec2 object.

Parameters:: angle – angle in radians, angle goes counter clockwise around the z-axis, x-axis = 0 deg.

vertices(angles: Iterable[float]) → Iterable[Vec2]

Yields vertices of the circle for iterable angles.

Parameters:: angles – iterable of angles as radians, angle goes counter-clockwise around the z-axis, x-axis = 0 deg.

flattening(sagitta: float) → Iterator[Vec2]: Approximate the circle by vertices, argument sagitta is the max. distance from the center of an arc segment to the center of its chord. Returns a closed polygon where the start vertex is coincident with the end vertex!

inside(point: UVec) → bool: Returns True if point is inside circle.

tangent(angle: float) → ConstructionRay

Returns tangent to circle at angle as ConstructionRay object.

Parameters:: angle – angle in radians

intersect_ray(ray: ConstructionRay, abs_tol: float = 1e-10) → Sequence[Vec2]

Returns intersection points of circle and ray as sequence of Vec2 objects.

Parameters:

ray – intersection ray
abs_tol – absolute tolerance for tests (e.g. test for tangents)

Returns:

tuple of Vec2 objects

tuple size	Description
0	no intersection
1	ray is a tangent to circle
2	ray intersects with the circle

intersect_line(line: ConstructionLine, abs_tol: float = 1e-10) → Sequence[Vec2]

Returns intersection points of circle and line as sequence of Vec2 objects.

Parameters:

line – intersection line
abs_tol – absolute tolerance for tests (e.g. test for tangents)

Returns:

tuple of Vec2 objects

tuple size	Description
0	no intersection
1	line intersects or touches the circle at one point
2	line intersects the circle at two points

intersect_circle(other: ConstructionCircle, abs_tol: float = 1e-10) → Sequence[Vec2]

Returns intersection points of two circles as sequence of Vec2 objects.

Parameters:

other – intersection circle
abs_tol – absolute tolerance for tests

Returns:

tuple of Vec2 objects

tuple size	Description
0	no intersection
1	circle touches the other circle at one point
2	circle intersects with the other circle

ConstructionArc

class ezdxf.math.ConstructionArc(center: UVec = (0, 0), radius: float = 1.0, start_angle: float = 0.0, end_angle: float = 360.0, is_counter_clockwise: bool | None = True)

Construction tool for 2D arcs.

ConstructionArc represents a 2D arc in the xy-plane, use an UCS to place a DXF Arc entity in 3D space, see method add_to_layout().

Implements the 2D transformation tools: translate(), scale_uniform() and rotate_z()

Parameters:

center – center point as Vec2 compatible object
radius – radius
start_angle – start angle in degrees
end_angle – end angle in degrees
is_counter_clockwise – swaps start- and end angle if False

center: center point as Vec2

radius: radius as float

start_angle: start angle in degrees

end_angle: end angle in degrees

angle_span: Returns angle span of arc from start- to end param.

start_angle_rad: Returns the start angle in radians.

end_angle_rad: Returns the end angle in radians.

start_point: start point of arc as Vec2.

end_point: end point of arc as Vec2.

bounding_box: bounding box of arc as BoundingBox2d.

angles(num: int) → Iterable[float]

Returns num angles from start- to end angle in degrees in counter-clockwise order.

All angles are normalized in the range from [0, 360).

vertices(a: Iterable[float]) → Iterable[Vec2]

Yields vertices on arc for angles in iterable a in WCS as location vectors.

Parameters:: a – angles in the range from 0 to 360 in degrees, arc goes counter clockwise around the z-axis, WCS x-axis = 0 deg.

tangents(a: Iterable[float]) → Iterable[Vec2]

Yields tangents on arc for angles in iterable a in WCS as direction vectors.

Parameters:: a – angles in the range from 0 to 360 in degrees, arc goes counter-clockwise around the z-axis, WCS x-axis = 0 deg.

translate(dx: float, dy: float) → ConstructionArc

Move arc about dx in x-axis and about dy in y-axis, returns self (floating interface).

Parameters:

dx – translation in x-axis
dy – translation in y-axis

scale_uniform(s: float) → ConstructionArc: Scale arc inplace uniform about s in x- and y-axis, returns self (floating interface).

rotate_z(angle: float) → ConstructionArc

Rotate arc inplace about z-axis, returns self (floating interface).

Parameters:: angle – rotation angle in degrees

classmethod from_2p_angle(start_point: UVec, end_point: UVec, angle: float, ccw: bool = True) → ConstructionArc

Create arc from two points and enclosing angle. Additional precondition: arc goes by default in counter-clockwise orientation from start_point to end_point, can be changed by ccw = False.

Parameters:

start_point – start point as Vec2 compatible object
end_point – end point as Vec2 compatible object
angle – enclosing angle in degrees
ccw – counter-clockwise direction if True

classmethod from_2p_radius(start_point: UVec, end_point: UVec, radius: float, ccw: bool = True, center_is_left: bool = True) → ConstructionArc

Create arc from two points and arc radius. Additional precondition: arc goes by default in counter-clockwise orientation from start_point to end_point can be changed by ccw = False.

The parameter center_is_left defines if the center of the arc is left or right of the line from start_point to end_point. Parameter ccw = False swaps start- and end point, which also inverts the meaning of center_is_left.

Parameters:

start_point – start point as Vec2 compatible object
end_point – end point as Vec2 compatible object
radius – arc radius
ccw – counter-clockwise direction if True
center_is_left – center point of arc is left of line from start- to end point if True

classmethod from_3p(start_point: UVec, end_point: UVec, def_point: UVec, ccw: bool = True) → ConstructionArc

Create arc from three points. Additional precondition: arc goes in counter-clockwise orientation from start_point to end_point.

Parameters:

start_point – start point as Vec2 compatible object
end_point – end point as Vec2 compatible object
def_point – additional definition point as Vec2 compatible object
ccw – counter-clockwise direction if True

add_to_layout(layout: BaseLayout, ucs: UCS | None = None, dxfattribs=None) → Arc

Add arc as DXF Arc entity to a layout.

Supports 3D arcs by using an UCS. An ConstructionArc is always defined in the xy-plane, but by using an arbitrary UCS, the arc can be placed in 3D space, automatically OCS transformation included.

Parameters:

layout – destination layout as BaseLayout object
ucs – place arc in 3D space by UCS object
dxfattribs – additional DXF attributes for the ARC entity

intersect_ray(ray: ConstructionRay, abs_tol: float = 1e-10) → Sequence[Vec2]

Returns intersection points of arc and ray as sequence of Vec2 objects.

Parameters:

ray – intersection ray
abs_tol – absolute tolerance for tests (e.g. test for tangents)

Returns:

tuple of Vec2 objects

tuple size	Description
0	no intersection
1	line intersects or touches the arc at one point
2	line intersects the arc at two points

intersect_line(line: ConstructionLine, abs_tol: float = 1e-10) → Sequence[Vec2]

Returns intersection points of arc and line as sequence of Vec2 objects.

Parameters:

line – intersection line
abs_tol – absolute tolerance for tests (e.g. test for tangents)

Returns:

tuple of Vec2 objects

tuple size	Description
0	no intersection
1	line intersects or touches the arc at one point
2	line intersects the arc at two points

intersect_circle(circle: ConstructionCircle, abs_tol: float = 1e-10) → Sequence[Vec2]

Returns intersection points of arc and circle as sequence of Vec2 objects.

Parameters:

circle – intersection circle
abs_tol – absolute tolerance for tests

Returns:

tuple of Vec2 objects

tuple size	Description
0	no intersection
1	circle intersects or touches the arc at one point
2	circle intersects the arc at two points

intersect_arc(other: ConstructionArc, abs_tol: float = 1e-10) → Sequence[Vec2]

Returns intersection points of two arcs as sequence of Vec2 objects.

Parameters:

other – other intersection arc
abs_tol – absolute tolerance for tests

Returns:

tuple of Vec2 objects

tuple size	Description
0	no intersection
1	other arc intersects or touches the arc at one point
2	other arc intersects the arc at two points

ConstructionEllipse

class ezdxf.math.ConstructionEllipse(center: UVec = NULLVEC, major_axis: UVec = X_AXIS, extrusion: UVec = Z_AXIS, ratio: float = 1, start_param: float = 0, end_param: float = math.tau, ccw: bool = True)

Construction tool for 3D ellipsis.

Parameters:

center – 3D center point
major_axis – major axis as 3D vector
extrusion – normal vector of ellipse plane
ratio – ratio of minor axis to major axis
start_param – start param in radians
end_param – end param in radians
ccw – is counter-clockwise flag - swaps start- and end param if False

center: center point as Vec3

major_axis: major axis as Vec3

minor_axis: minor axis as Vec3, automatically calculated from major_axis and extrusion.

extrusion: extrusion vector (normal of ellipse plane) as Vec3

ratio: ratio of minor axis to major axis (float)

start: start param in radians (float)

end: end param in radians (float)

start_point: Returns start point of ellipse as Vec3.

end_point: Returns end point of ellipse as Vec3.

property param_span: float: Returns the counter-clockwise params span from start- to end param, see also ezdxf.math.ellipse_param_span() for more information.

to_ocs() → ConstructionEllipse

Returns ellipse parameters as OCS representation.

OCS elevation is stored in center.z.

params(num: int) → Iterable[float]

Returns num params from start- to end param in counter-clockwise order.

All params are normalized in the range from [0, 2π).

vertices(params: Iterable[float]) → Iterable[Vec3]

Yields vertices on ellipse for iterable params in WCS.

Parameters:: params – param values in the range from [0, 2π) in radians, param goes counter-clockwise around the extrusion vector, major_axis = local x-axis = 0 rad.

flattening(distance: float, segments: int = 4) → Iterable[Vec3]

Adaptive recursive flattening. The argument segments is the minimum count of approximation segments, if the distance from the center of the approximation segment to the curve is bigger than distance the segment will be subdivided. Returns a closed polygon for a full ellipse: start vertex == end vertex.

Parameters:

distance – maximum distance from the projected curve point onto the segment chord.
segments – minimum segment count

params_from_vertices(vertices: Iterable[UVec]) → Iterable[float]

Yields ellipse params for all given vertices.

The vertex don’t have to be exact on the ellipse curve or in the range from start- to end param or even in the ellipse plane. Param is calculated from the intersection point of the ray projected on the ellipse plane from the center of the ellipse through the vertex.

Warning

An input for start- and end vertex at param 0 and 2π return unpredictable results because of floating point inaccuracy, sometimes 0 and sometimes 2π.

dxfattribs() → dict[str, Any]

Returns required DXF attributes to build an ELLIPSE entity.

Entity ELLIPSE has always a ratio in range from 1e-6 to 1.

main_axis_points() → Iterable[Vec3]: Yields main axis points of ellipse in the range from start- to end param.

classmethod from_arc(center: UVec = NULLVEC, radius: float = 1, extrusion: UVec = Z_AXIS, start_angle: float = 0, end_angle: float = 360, ccw: bool = True) → ConstructionEllipse

Returns ConstructionEllipse from arc or circle.

Arc and Circle parameters defined in OCS.

Parameters:

center – center in OCS
radius – arc or circle radius
extrusion – OCS extrusion vector
start_angle – start angle in degrees
end_angle – end angle in degrees
ccw – arc curve goes counter clockwise from start to end if True

transform(m: Matrix44) → None: Transform ellipse in place by transformation matrix m.

swap_axis() → None: Swap axis and adjust start- and end parameter.

add_to_layout(layout: BaseLayout, dxfattribs=None) → Ellipse

Add ellipse as DXF Ellipse entity to a layout.

Parameters:

layout – destination layout as BaseLayout object
dxfattribs – additional DXF attributes for the ELLIPSE entity

ConstructionBox

class ezdxf.math.ConstructionBox(center: UVec = (0, 0), width: float = 1, height: float = 1, angle: float = 0)

Construction tool for 2D rectangles.

Parameters:

center – center of rectangle
width – width of rectangle
height – height of rectangle
angle – angle of rectangle in degrees

center: box center

width: box width

height: box height

angle: rotation angle in degrees

corners: box corners as sequence of Vec2 objects.

bounding_box: BoundingBox2d

incircle_radius: incircle radius

circumcircle_radius: circum circle radius

__iter__() → Iterable[Vec2]: Iterable of box corners as Vec2 objects.

__getitem__(corner) → Vec2: Get corner by index corner, list like slicing is supported.

__repr__() → str: Returns string representation of box as ConstructionBox(center, width, height, angle)

classmethod from_points(p1: UVec, p2: UVec) → ConstructionBox

Creates a box from two opposite corners, box sides are parallel to x- and y-axis.

Parameters:

p1 – first corner as Vec2 compatible object
p2 – second corner as Vec2 compatible object

translate(dx: float, dy: float) → None

Move box about dx in x-axis and about dy in y-axis.

Parameters:

dx – translation in x-axis
dy – translation in y-axis

expand(dw: float, dh: float) → None: Expand box: dw expand width, dh expand height.

scale(sw: float, sh: float) → None: Scale box: sw scales width, sh scales height.

rotate(angle: float) → None: Rotate box by angle in degrees.

is_inside(point: UVec) → bool: Returns True if point is inside of box.

is_any_corner_inside(other: ConstructionBox) → bool: Returns True if any corner of other box is inside this box.

is_overlapping(other: ConstructionBox) → bool: Returns True if this box and other box do overlap.

border_lines() → Sequence[ConstructionLine]: Returns borderlines of box as sequence of ConstructionLine.

intersect(line: ConstructionLine) → list[Vec2]

Returns 0, 1 or 2 intersection points between line and box borderlines.

Parameters:

line – line to intersect with borderlines

Returns:

list of intersection points

list size	Description
0	no intersection
1	line touches box at one corner
2	line intersects with box

ConstructionPolyline

class ezdxf.math.ConstructionPolyline(vertices: Iterable[UVec], close: bool = False, rel_tol: float = REL_TOL)

Construction tool for 3D polylines.

A polyline construction tool to measure, interpolate and divide anything that can be approximated or flattened into vertices. This is an immutable data structure which supports the Sequence interface.

Parameters:

vertices – iterable of polyline vertices
close – True to close the polyline (first vertex == last vertex)
rel_tol – relative tolerance for floating point comparisons

Example to measure or divide a SPLINE entity:

import ezdxf
from ezdxf.math import ConstructionPolyline

doc = ezdxf.readfile("your.dxf")
msp = doc.modelspace()
spline = msp.query("SPLINE").first
if spline is not None:
    polyline = ConstructionPolyline(spline.flattening(0.01))
    print(f"Entity {spline} has an approximated length of {polyline.length}")
    # get dividing points with a distance of 1.0 drawing unit to each other
    points = list(polyline.divide_by_length(1.0))

property length: float: Returns the overall length of the polyline.

property is_closed: bool: Returns True if the polyline is closed (first vertex == last vertex).

data(index: int) → tuple[float, float, Vec3]: Returns the tuple (distance from start, distance from previous vertex, vertex). All distances measured along the polyline.

index_at(distance: float) → int: Returns the data index of the exact or next data entry for the given distance. Returns the index of last entry if distance > length.

vertex_at(distance: float) → Vec3: Returns the interpolated vertex at the given distance from the start of the polyline.

divide(count: int) → Iterator[Vec3]: Returns count interpolated vertices along the polyline. Argument count has to be greater than 2 and the start- and end vertices are always included.

divide_by_length(length: float, force_last: bool = False) → Iterator[Vec3]: Returns interpolated vertices along the polyline. Each vertex has a fix distance length from its predecessor. Yields the last vertex if argument force_last is True even if the last distance is not equal to length.

Shape2d

class ezdxf.math.Shape2d(vertices: Iterable[UVec] | None = None)

Construction tools for 2D shapes.

A 2D geometry object as list of Vec2 objects, vertices can be moved, rotated and scaled.

Parameters:: vertices – iterable of Vec2 compatible objects.

vertices: List of Vec2 objects

bounding_box: Returns the bounding box of the shape.

__len__() → int: Returns count of vertices.

__getitem__(item: int) → Vec2
__getitem__(item: slice) → list[Vec2]: Get vertex by index item, supports list like slicing.

append(vertex: UVec) → None

Append single vertex.

Parameters:: vertex – vertex as Vec2 compatible object

extend(vertices: Iterable[UVec]) → None

Append multiple vertices.

Parameters:: vertices – iterable of vertices as Vec2 compatible objects

translate(vector: UVec) → None: Translate shape about vector.

scale(sx: float = 1.0, sy: float = 1.0) → None: Scale shape about sx in x-axis and sy in y-axis.

scale_uniform(scale: float) → None: Scale shape uniform about scale in x- and y-axis.

rotate(angle: float, center: UVec | None = None) → None: Rotate shape around rotation center about angle in degrees.

rotate_rad(angle: float, center: UVec | None = None) → None: Rotate shape around rotation center about angle in radians.

offset(offset: float, closed: bool = False) → Shape2d

Returns a new offset shape, for more information see also ezdxf.math.offset_vertices_2d() function.

Parameters:

offset – line offset perpendicular to direction of shape segments defined by vertices order, offset > 0 is ‘left’ of line segment, offset < 0 is ‘right’ of line segment
closed – True to handle as closed shape

convex_hull() → Shape2d: Returns convex hull as new shape.

Curves

`ApproxParamT`	Approximation tool for parametrized curves.
`BSpline`	B-spline construction tool.
`Bezier`	Generic Bézier curve of any degree.
`Bezier3P`	Implements an optimized quadratic Bézier curve for exact 3 control points.
`Bezier4P`	Implements an optimized cubic Bézier curve for exact 4 control points.
`EulerSpiral`	This class represents an euler spiral (clothoid) for curvature (Radius of curvature).

BSpline

class ezdxf.math.BSpline(control_points: Iterable[UVec], order: int = 4, knots: Iterable[float] | None = None, weights: Iterable[float] | None = None)

B-spline construction tool.

Internal representation of a B-spline curve. The default configuration of the knot vector is a uniform open knot vector (“clamped”).

Factory functions:

fit_points_to_cad_cv()

fit_points_to_cubic_bezier()

open_uniform_bspline()

closed_uniform_bspline()

rational_bspline_from_arc()

rational_bspline_from_ellipse()

global_bspline_interpolation()

local_cubic_bspline_interpolation()

Parameters:

control_points – iterable of control points as Vec3 compatible objects
order – spline order (degree + 1)
knots – iterable of knot values
weights – iterable of weight values

property control_points: Sequence[Vec3]: Control points as tuple of Vec3

property count: int: Count of control points, (n + 1 in text book notation).

property order: int: Order (k) of B-spline = p + 1

property degree: int: Degree (p) of B-spline = order - 1

property max_t: float: Biggest knot value.

property is_rational: Returns True if curve is a rational B-spline. (has weights)

property is_clamped: Returns True if curve is a clamped (open) B-spline.

knots() → Sequence[float]: Returns a tuple of knot values as floats, the knot vector always has order + count values (n + p + 2 in text book notation).

weights() → Sequence[float]: Returns a tuple of weights values as floats, one for each control point or an empty tuple.

params(segments: int) → Iterable[float]: Yield evenly spaced parameters for given segment count.

reverse() → BSpline: Returns a new BSpline object with reversed control point order.

transform(m: Matrix44) → BSpline: Returns a new BSpline object transformed by a Matrix44 transformation matrix.

approximate(segments: int = 20) → Iterable[Vec3]: Approximates curve by vertices as Vec3 objects, vertices count = segments + 1.

flattening(distance: float, segments: int = 4) → Iterator[Vec3]

Adaptive recursive flattening. The argument segments is the minimum count of approximation segments between two knots, if the distance from the center of the approximation segment to the curve is bigger than distance the segment will be subdivided.

Parameters:

distance – maximum distance from the projected curve point onto the segment chord.
segments – minimum segment count between two knots

point(t: float) → Vec3

Returns point for parameter t.

Parameters:: t – parameter in range [0, max_t]

points(t: Iterable[float]) → Iterable[Vec3]

Yields points for parameter vector t.

Parameters:: t – parameters in range [0, max_t]

derivative(t: float, n: int = 2) → list[Vec3]

Return point and derivatives up to n <= degree for parameter t.

e.g. n=1 returns point and 1st derivative.

Parameters:

t – parameter in range [0, max_t]
n – compute all derivatives up to n <= degree

Returns:

n+1 values as Vec3 objects

derivatives(t: Iterable[float], n: int = 2) → Iterable[list[Vec3]]

Yields points and derivatives up to n <= degree for parameter vector t.

e.g. n=1 returns point and 1st derivative.

Parameters:

t – parameters in range [0, max_t]
n – compute all derivatives up to n <= degree

Returns:

List of n+1 values as Vec3 objects

insert_knot(t: float) → BSpline

Insert an additional knot, without altering the shape of the curve. Returns a new BSpline object.

Parameters:: t – position of new knot 0 < t < max_t

knot_refinement(u: Iterable[float]) → BSpline

Insert multiple knots, without altering the shape of the curve. Returns a new BSpline object.

Parameters:: u – vector of new knots t and for each t: 0 < t < max_t

static from_ellipse(ellipse: ConstructionEllipse) → BSpline: Returns the ellipse as BSpline of 2nd degree with as few control points as possible.

static from_arc(arc: ConstructionArc) → BSpline: Returns the arc as BSpline of 2nd degree with as few control points as possible.

static from_fit_points(points: Iterable[UVec], degree=3, method='chord') → BSpline: Returns BSpline defined by fit points.

static arc_approximation(arc: ConstructionArc, num: int = 16) → BSpline: Returns an arc approximation as BSpline with num control points.

static ellipse_approximation(ellipse: ConstructionEllipse, num: int = 16) → BSpline: Returns an ellipse approximation as BSpline with num control points.

bezier_decomposition() → Iterable[list[Vec3]]

Decompose a non-rational B-spline into multiple Bézier curves.

This is the preferred method to represent the most common non-rational B-splines of 3rd degree by cubic Bézier curves, which are often supported by render backends.

Returns:: Yields control points of Bézier curves, each Bézier segment has degree+1 control points e.g. B-spline of 3rd degree yields cubic Bézier curves of 4 control points.

cubic_bezier_approximation(level: int = 3, segments: int | None = None) → Iterable[Bezier4P]

Approximate arbitrary B-splines (degree != 3 and/or rational) by multiple segments of cubic Bézier curves. The choice of cubic Bézier curves is based on the widely support of this curves by many render backends. For cubic non-rational B-splines, which is maybe the most common used B-spline, is bezier_decomposition() the better choice.

approximation by level: an educated guess, the first level of approximation segments is based on the count of control points and their distribution along the B-spline, every additional level is a subdivision of the previous level.

E.g. a B-Spline of 8 control points has 7 segments at the first level, 14 at the 2nd level and 28 at the 3rd level, a level >= 3 is recommended.

approximation by a given count of evenly distributed approximation segments.

Parameters:

level – subdivision level of approximation segments (ignored if argument segments is not None)
segments – absolute count of approximation segments

Returns:

Yields control points of cubic Bézier curves as Bezier4P objects

degree_elevation(t: int) → BSpline

Returns a new BSpline with a t-times elevated degree.

Degree elevation increases the degree of a curve without changing the shape of the curve. This method implements the algorithm A5.9 of the “The NURBS Book” by Piegl & Tiller.

Added in version 1.4.

point_inversion(point: UVec, *, epsilon=1e-8, max_iterations=100, init=8) → float

Returns the parameter t for a point on the curve that is closest to the input point.

This is an iterative search using Newton’s method, so there is no guarantee of success, especially for splines with many turns.

Parameters:

point (UVec) – point on the curve or near the curve
epsilon (float) – desired precision (distance input point to point on curve)
max_iterations (int) – max iterations for Newton’s method
init (int) – number of points to calculate in the initialization phase

Added in version 1.4.

measure(segments: int = 100) → Measurement

Returns a B-spline measurement tool.

All measurements are based on the approximated curve.

Parameters:: segments – count of segments for B-spline approximation.

Added in version 1.4.

split(t: float) → tuple[BSpline, BSpline]

Splits the B-spline at parameter t and returns two new B-splines.

Raises:: ValuerError – t out of range 0 < t < max_t

Added in version 1.4.

class ezdxf.math.bspline.Measurement(spline: BSpline, segments: int)

B-spline measurement tool.

All measurements are based on the approximated curve.

Added in version 1.4.

extmin: minimum extents of the approximated curve as Vec3

extmax: maximum extents of the approximated curve as Vec3

property length: float: Returns the approximated length of the B-spline.

distance(t: float) → float: Returns the distance along the curve from the start point for then given parameter t.

param_at(distance: float) → float: Returns the parameter t for a given distance along the curve from the start point.

divide(count: int) → list[float]

Returns the interpolated B-spline parameters for dividing the curve into count segments of equal length.

The method yields only the dividing parameters, the first (0.0) and last parameter (max_t) are not included e.g. dividing a B-spline by 3 yields two parameters [t1, t2] that divides the B-spline into 3 parts of equal length.

Bezier

class ezdxf.math.Bezier(defpoints: Iterable[UVec])

Generic Bézier curve of any degree.

A Bézier curve is a parametric curve used in computer graphics and related fields. Bézier curves are used to model smooth curves that can be scaled indefinitely. “Paths”, as they are commonly referred to in image manipulation programs, are combinations of linked Bézier curves. Paths are not bound by the limits of rasterized images and are intuitive to modify. (Source: Wikipedia)

This is a generic implementation which works with any count of definition points greater than 2, but it is a simple and slow implementation. For more performance look at the specialized Bezier4P and Bezier3P classes.

Objects are immutable.

Parameters:: defpoints – iterable of definition points as Vec3 compatible objects.

control_points: Control points as tuple of Vec3 objects.

params(segments: int) → Iterable[float]: Yield evenly spaced parameters from 0 to 1 for given segment count.

reverse() → Bezier: Returns a new Bèzier-curve with reversed control point order.

transform(m: Matrix44) → Bezier

General transformation interface, returns a new Bezier curve.

Parameters:: m – 4x4 transformation matrix (ezdxf.math.Matrix44)

approximate(segments: int = 20) → Iterable[Vec3]: Approximates curve by vertices as Vec3 objects, vertices count = segments + 1.

flattening(distance: float, segments: int = 4) → Iterable[Vec3]

Adaptive recursive flattening. The argument segments is the minimum count of approximation segments, if the distance from the center of the approximation segment to the curve is bigger than distance the segment will be subdivided.

Parameters:

distance – maximum distance from the center of the curve (Cn) to the center of the linear (C1) curve between two approximation points to determine if a segment should be subdivided.
segments – minimum segment count

point(t: float) → Vec3: Returns a point for parameter t in range [0, 1] as Vec3 object.

points(t: Iterable[float]) → Iterable[Vec3]: Yields multiple points for parameters in vector t as Vec3 objects. Parameters have to be in range [0, 1].

derivative(t: float) → tuple[Vec3, Vec3, Vec3]: Returns (point, 1st derivative, 2nd derivative) tuple for parameter t in range [0, 1] as Vec3 objects.

derivatives(t: Iterable[float]) → Iterable[tuple[Vec3, Vec3, Vec3]]: Returns multiple (point, 1st derivative, 2nd derivative) tuples for parameter vector t as Vec3 objects. Parameters in range [0, 1]

Bezier4P

class ezdxf.math.Bezier4P(defpoints: Sequence[T])

Implements an optimized cubic Bézier curve for exact 4 control points.

A Bézier curve is a parametric curve, parameter t goes from 0 to 1, where 0 is the first control point and 1 is the fourth control point.

The class supports points of type Vec2 and Vec3 as input, the class instances are immutable.

Parameters:: defpoints – sequence of definition points as Vec2 or Vec3 compatible objects.

control_points: Control points as tuple of Vec3 or Vec2 objects.

reverse() → Bezier4P[T]: Returns a new Bèzier-curve with reversed control point order.

transform(m: Matrix44) → Bezier4P[Vec3]

General transformation interface, returns a new Bezier4p curve as a 3D curve.

Parameters:: m – 4x4 transformation Matrix44

approximate(segments: int) → Iterator[T]

Approximate Bézier curve by vertices, yields segments + 1 vertices as (x, y[, z]) tuples.

Parameters:: segments – count of segments for approximation

flattening(distance: float, segments: int = 4) → Iterator[T]

Adaptive recursive flattening. The argument segments is the minimum count of approximation segments, if the distance from the center of the approximation segment to the curve is bigger than distance the segment will be subdivided.

Parameters:

distance – maximum distance from the center of the cubic (C3) curve to the center of the linear (C1) curve between two approximation points to determine if a segment should be subdivided.
segments – minimum segment count

approximated_length(segments: int = 128) → float: Returns estimated length of Bèzier-curve as approximation by line segments.

point(t: float) → T

Returns point for location t at the Bèzier-curve.

Parameters:: t – curve position in the range [0, 1]

tangent(t: float) → T

Returns direction vector of tangent for location t at the Bèzier-curve.

Parameters:: t – curve position in the range [0, 1]

Bezier3P

class ezdxf.math.Bezier3P(defpoints: Sequence[T])

Implements an optimized quadratic Bézier curve for exact 3 control points.

The class supports points of type Vec2 and Vec3 as input, the class instances are immutable.

Parameters:: defpoints – sequence of definition points as Vec2 or Vec3 compatible objects.

control_points: Control points as tuple of Vec3 or Vec2 objects.

reverse() → Bezier3P[T]: Returns a new Bèzier-curve with reversed control point order.

transform(m: Matrix44) → Bezier3P[Vec3]

General transformation interface, returns a new Bezier3P curve and it is always a 3D curve.

Parameters:: m – 4x4 transformation Matrix44

approximate(segments: int) → Iterator[T]

Approximate Bézier curve by vertices, yields segments + 1 vertices as (x, y[, z]) tuples.

Parameters:: segments – count of segments for approximation

flattening(distance: float, segments: int = 4) → Iterator[T]

Adaptive recursive flattening. The argument segments is the minimum count of approximation segments, if the distance from the center of the approximation segment to the curve is bigger than distance the segment will be subdivided.

Parameters:

distance – maximum distance from the center of the quadratic (C2) curve to the center of the linear (C1) curve between two approximation points to determine if a segment should be subdivided.
segments – minimum segment count

approximated_length(segments: int = 128) → float: Returns estimated length of Bèzier-curve as approximation by line segments.

point(t: float) → T

Returns point for location t at the Bèzier-curve.

Parameters:: t – curve position in the range [0, 1]

tangent(t: float) → T

Returns direction vector of tangent for location t at the Bèzier-curve.

Parameters:: t – curve position in the range [0, 1]

ApproxParamT

class ezdxf.math.ApproxParamT(curve, *, max_t: float = 1.0, segments: int = 100)

Approximation tool for parametrized curves.

approximate parameter t for a given distance from the start of the curve
approximate the distance for a given parameter t from the start of the curve

These approximations can be applied to all parametrized curves which provide a point() method, like Bezier4P, Bezier3P and BSpline.

The approximation is based on equally spaced parameters from 0 to max_t for a given segment count. The flattening() method can not be used for the curve approximation, because the required parameter t is not logged by the flattening process.

Parameters:

curve – curve object, requires a method point()
max_t – the max. parameter value
segments – count of approximation segments

property max_t: float

property polyline: ConstructionPolyline

param_t(distance: float): Approximate parameter t for the given distance from the start of the curve.

distance(t: float) → float: Approximate the distance from the start of the curve to the point t on the curve.

EulerSpiral

class ezdxf.math.EulerSpiral(curvature: float = 1.0)

This class represents an euler spiral (clothoid) for curvature (Radius of curvature).

This is a parametric curve, which always starts at the origin = (0, 0).

Parameters:: curvature – radius of curvature

radius(t: float) → float: Get radius of circle at distance t.

tangent(t: float) → Vec3: Get tangent at distance t as Vec3 object.

distance(radius: float) → float: Get distance L from origin for radius.

point(t: float) → Vec3: Get point at distance t as Vec3.

circle_center(t: float) → Vec3: Get circle center at distance t.

approximate(length: float, segments: int) → Iterable[Vec3]: Approximate curve of length with line segments. Generates segments+1 vertices as Vec3 objects.

bspline(length: float, segments: int = 10, degree: int = 3, method: str = 'uniform') → BSpline

Approximate euler spiral as B-spline.

Parameters:

length – length of euler spiral
segments – count of fit points for B-spline calculation
degree – degree of BSpline
method – calculation method for parameter vector t

Returns:

BSpline