PyCSG

Constructive Solid Geometry (CSG) is a modeling technique that uses Boolean operations like union and intersection to combine 3D solids. This library implements CSG operations on meshes elegantly and concisely using BSP trees, and is meant to serve as an easily understandable implementation of the algorithm. All edge cases involving overlapping coplanar polygons in both solids are correctly handled.

Example for usage:

import ezdxf
from ezdxf.render.forms import cube, cylinder_2p
from ezdxf.addons.pycsg import CSG

# create new DXF document
doc = ezdxf.new()
msp = doc.modelspace()

# create same geometric primitives as MeshTransformer() objects
cube1 = cube()
cylinder1 = cylinder_2p(count=32, base_center=(0, -1, 0), top_center=(0, 1, 0), radius=.25)

# build solid union
union = CSG(cube1) + CSG(cylinder1)
# convert to mesh and render mesh to modelspace
union.mesh().render_mesh(msp, dxfattribs={'color': 1})

# build solid difference
difference = CSG(cube1) - CSG(cylinder1)
# convert to mesh, translate mesh and render mesh to modelspace
difference.mesh().translate(1.5).render_mesh(msp, dxfattribs={'color': 3})

# build solid intersection
intersection = CSG(cube1) * CSG(cylinder1)
# convert to mesh, translate mesh and render mesh to modelspace
intersection.mesh().translate(2.75).render_mesh(msp, dxfattribs={'color': 5})

doc.saveas('csg.dxf')
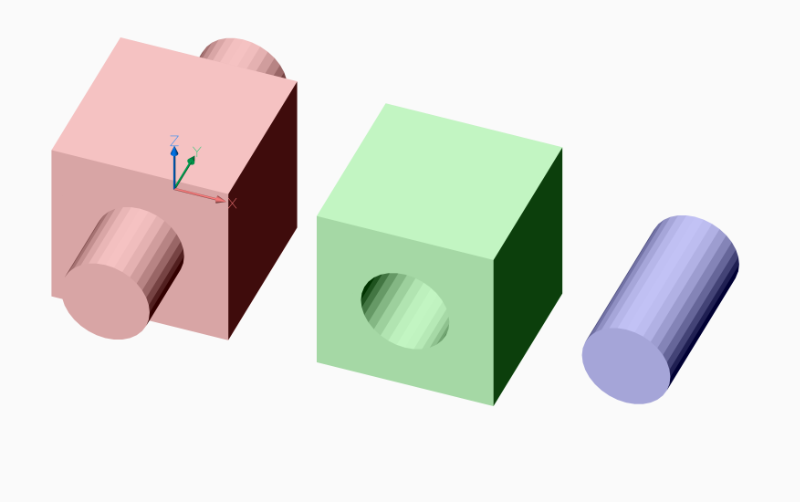
Cube vs Cylinder

This CSG kernel supports only meshes as MeshBuilder objects, which can be created from and converted to DXF Mesh entities.

This CSG kernel is not compatible with ACIS objects like Solid3d, Body, Surface or Region.

Note

This is a pure Python implementation, don’t expect great performance and the implementation is based on an unbalanced BSP tree, so in the case of RecursionError, increase the recursion limit:

import sys

actual_limit = sys.getrecursionlimit()
# default is 1000, increasing too much may cause a seg fault
sys.setrecursionlimit(10000)

...  # do the CSG stuff

sys.setrecursionlimit(actual_limit)

CSG works also with spheres, but with really bad runtime behavior and most likely RecursionError exceptions, and use quadrilaterals as body faces to reduce face count by setting argument quads to True.

import ezdxf

from ezdxf.render.forms import sphere, cube
from ezdxf.addons.pycsg import CSG

doc = ezdxf.new()
doc.set_modelspace_vport(6, center=(5, 0))
msp = doc.modelspace()

cube1 = cube().translate(-.5, -.5, -.5)
sphere1 = sphere(count=32, stacks=16, radius=.5, quads=True)

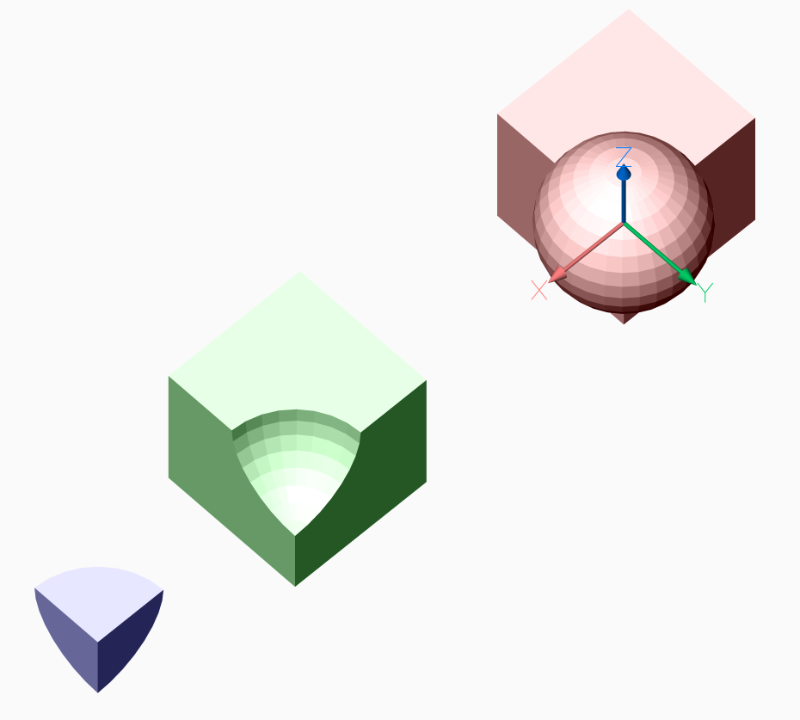
union = (CSG(cube1) + CSG(sphere1)).mesh()
union.render_mesh(msp, dxfattribs={'color': 1})

subtract = (CSG(cube1) - CSG(sphere1)).mesh().translate(2.5)
subtract.render_mesh(msp, dxfattribs={'color': 3})

intersection = (CSG(cube1) * CSG(sphere1)).mesh().translate(4)
intersection.render_mesh(msp, dxfattribs={'color': 5})
Cube vs Sphere

Hard Core CSG - Menger Sponge Level 3 vs Sphere

Required runtime on an old Xeon E5-1620 Workstation @ 3.60GHz (2020), with default recursion limit of 1000 on Windows 10:

  • CPython 3.8.1 64bit: ~60 seconds,

  • PyPy [PyPy 7.2.0] 32bit: ~6 seconds, and using __slots__ reduced runtime below 5 seconds, yes - PyPy is worth a look for long running scripts!

Updated runtime in 2024 on an i7-12700K @ 3.60GHz (peak ~5GHz), Windows 11:

  • CPython 3.11.6 64bit: ~3.4 seconds

  • PyPy 3.9.18 [PyPy 7.3.13] 64bit: ~1.5 seconds

from ezdxf.render.forms import sphere
from ezdxf.addons import MengerSponge
from ezdxf.addons.pycsg import CSG

doc = ezdxf.new()
doc.layers.new('sponge', dxfattribs={'color': 5})
doc.layers.new('sphere', dxfattribs={'color': 6})

doc.set_modelspace_vport(6, center=(5, 0))
msp = doc.modelspace()

sponge1 = MengerSponge(level=3).mesh()
sphere1 = sphere(count=32, stacks=16, radius=.5, quads=True).translate(.25, .25, 1)

subtract = (CSG(sponge1, meshid=1) - CSG(sphere1, meshid=2))
# get mesh result by id
subtract.mesh(1).render_mesh(msp, dxfattribs={'layer': 'sponge'})
subtract.mesh(2).render_mesh(msp, dxfattribs={'layer': 'sphere'})
Menger Sponge vs Sphere

CSG Class

class ezdxf.addons.pycsg.CSG(mesh: MeshBuilder, meshid: int = 0)

Constructive Solid Geometry (CSG) is a modeling technique that uses Boolean operations like union and intersection to combine 3D solids. This class implements CSG operations on meshes.

New 3D solids are created from MeshBuilder objects and results can be exported as MeshTransformer objects to ezdxf by method mesh().

Parameters:

  • mesh – ezdxf.render.MeshBuilder or inherited object

  • meshid – individual mesh ID to separate result meshes, 0 is default

mesh(meshid: int = 0) → MeshTransformer

Returns a ezdxf.render.MeshTransformer object.

Parameters:

meshid – individual mesh ID, 0 is default

union(other: CSG) → CSG

Return a new CSG solid representing space in either this solid or in the solid other. Neither this solid nor the solid other are modified:

A.union(B)

+-------+            +-------+
|       |            |       |
|   A   |            |       |
|    +--+----+   =   |       +----+
+----+--+    |       +----+       |
     |   B   |            |       |
     |       |            |       |
     +-------+            +-------+
__add__()
union = A + B
subtract(other: CSG) → CSG

Return a new CSG solid representing space in this solid but not in the solid other. Neither this solid nor the solid other are modified:

A.subtract(B)

+-------+            +-------+
|       |            |       |
|   A   |            |       |
|    +--+----+   =   |    +--+
+----+--+    |       +----+
     |   B   |
     |       |
     +-------+
__sub__()
difference = A - B
intersect(other: CSG) → CSG

Return a new CSG solid representing space both this solid and in the solid other. Neither this solid nor the solid other are modified:

A.intersect(B)

+-------+
|       |
|   A   |
|    +--+----+   =   +--+
+----+--+    |       +--+
     |   B   |
     |       |
     +-------+
__mul__()
intersection = A * B
inverse() → CSG

Return a new CSG solid with solid and empty space switched. This solid is not modified.

License

  • Original implementation csg.js, Copyright (c) 2011 Evan Wallace (http://madebyevan.com/), under the MIT license.

  • Python port pycsg, Copyright (c) 2012 Tim Knip (http://www.floorplanner.com), under the MIT license.

  • Additions by Alex Pletzer (Pennsylvania State University)

  • Integration as ezdxf add-on, Copyright (c) 2020, Manfred Moitzi, MIT License.